Negative NumbersとSigned Negator【Turing Complete編】
目次
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
Negative Numbersステージ
当ステージでは負の数が登場します。
最上位ビットを-128(=27)とすることで、8ビットが-128~127の整数値を扱えるようになります。

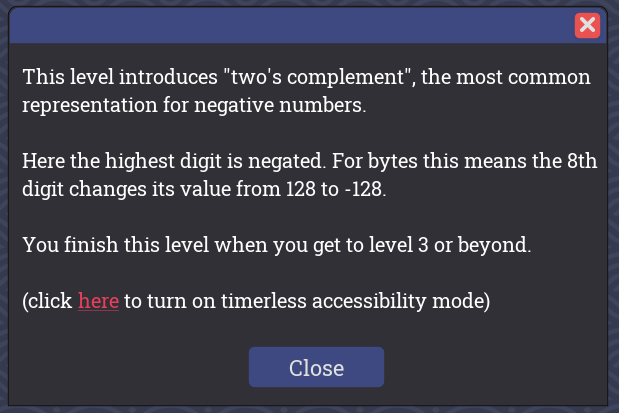
問題が次々に出題され、下のON・OFFを操作して、レベル3以上を達成すればクリアになります。
全部ONにすると-1(=-128+127)になることです。ポイントはこれを基点にして、1をOFFにすれば-2になり、2をOFFにすれば-3になります。つまり、最上位ビットがONであれば、残りのビットにてOFFになる数が増えていけば、マイナス側に大きくなっていきます。
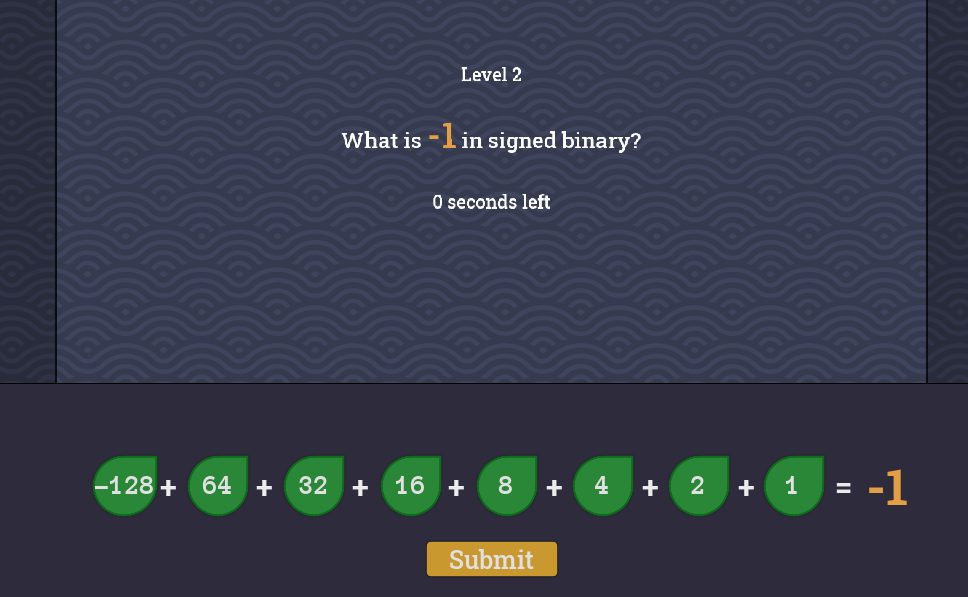
クリアするとLevel mapから次の問題(Signed Negatorの問題)が解放されます。


補数を理解しよう
半減算器
半減算器(half subtracter)とは、減算をする回路です。ただし、桁借りを意味する入力はありません。
※加算器には半加算器と全加算器があったように、減算器にも半減算器と全減算器があります。
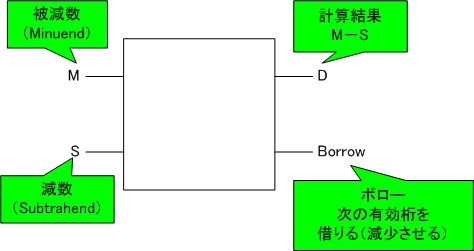
真理値表
| M | S | D | Borrow |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
回路
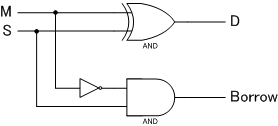
全減算器
全減算器のブロック図は次の通りです。

真理値表
| Bin (S’) | M | S | D1 (M’) | B1 | D | B2 | Bout |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
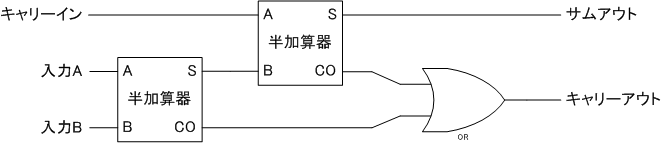
半加算器で全加算器を構築する
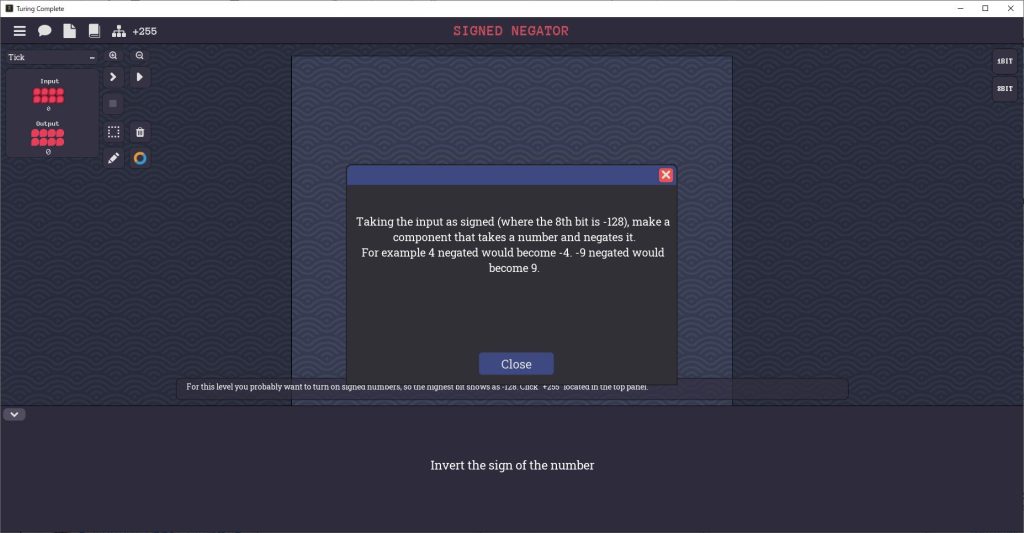
Signed Negatorステージ
Signed Negatorステージのゴールは、入力の値(符号つきの整数)の正負を反転させた値を出力する回路を組むことです。
入力が正の数なら負の数に変換して出力し、入力が負の数なら正の数に変換して出力します。
Signed Negatorステージを解く
1:符号を反転させる回路を設計する
符号を反転させた値は、2の補数であることを解説しました。
そして、2の補数を得るには、全ビット反転してから1を足すことで実現できることも言及しました。
2:使えるコンポーネントを把握する
これまで登場したコンポーネントを思い出して、使えそうなものを考えてください。
・8ビットを全ビット反転⇒Turing Completeでいえば、8 Bit NOTコンポーネント。
・8ビットに1を足す⇒(8ビット用の)全加算器。Turing Completeでいえば、Addコンポーネント。
右上の[1BIT]と[8BIT]アイコンを押して、使えるコンポーネントを確認します。


・[8BIT]アイコン>[MATH]アイコン>[ADD]アイコン・・・これがAddコンポーネント。
・[1BIT]アイコン>[N]アイコン・・・これがNOTコンポーネント。
各コンポーネントの入出力を再確認します。
※大きいピンは8ビット用、小さいピンは1ビット用です。


3:内部回路を実装する
前段では8 Bit NOTコンポーネントに通して全ビット反転させます。それを後段のAddコンポーネントのInput 1に入れます。
また、Input 2は1固定を加えます。ただし、Input 2は大きいピンであり、直接ONコンポーネントをつなげられません。ビット数が合わないからです。そこで、8 Bit Makerを通してから接続します。
後は、Addコンポーネントの出力をそのまま出力ピンにつなげるだけです。
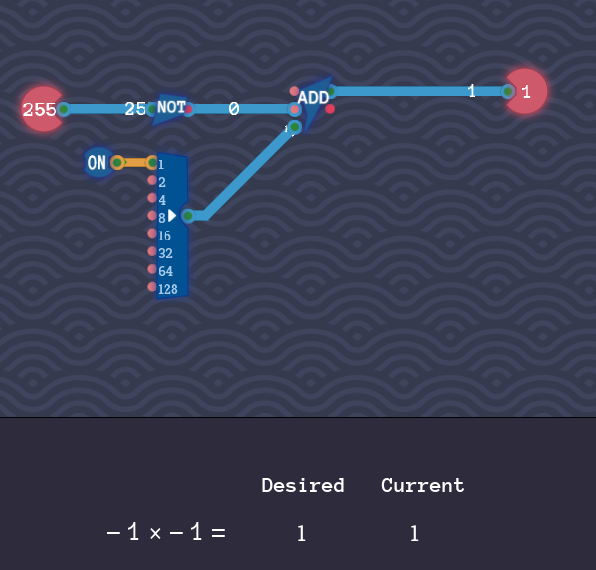
4:テストする
テストにパスすると、Negate(Signed Negator)コンポーネントがアンロックします。
なお、左上のLevel mapの右側の数値をクリックするたびに、交互に「+255」と「-1」に切り替わります。これは8ビット値の正負の表現法になります。最上位ビットをどう扱うかの切り替えになります。
「+255」にすると、符号なしの8ビット値、すなわち正の数だけを扱います。一方、「-1」にすると、符号ありの8ビット値、すなわち正負の数として扱います。
Addコンポーネントのキャリーインを利用する【別解】
Input 2に1を加えていますが、8ビットにするためにわざわざ8 Bit Makerを用いています。
Addコンポーネントのキャリーインは桁上げようですが、これをインクリメント用に代用する方法があります。
キャリーインとONコンポーネントはどちらも1ビットであり、直接をつなげられます。
これを実現した回路は次の通りです。
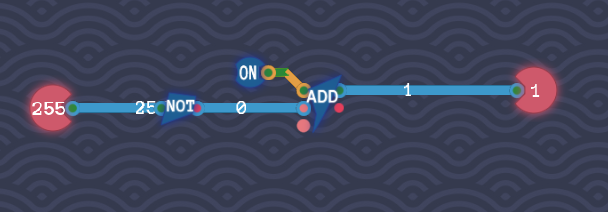
※先ほどの回路と比べてすっきりしましたが、これはキャリーインの役割を無視した使い方です。あくまで先の回路が基本であることを念頭においてください。