Masking Time【Turing Complete編】

2023年9月12日

Masking Timeステージ

要求している内容は後述しますが、Masking Timeステージのゴールは入力を4で割った余りを計算することです。

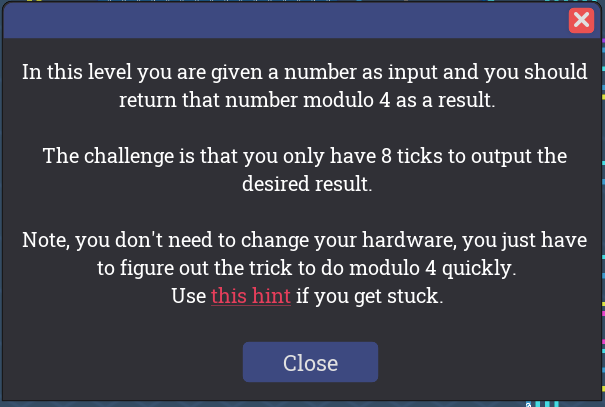
提示されたヒントは次の通りです。

Level log

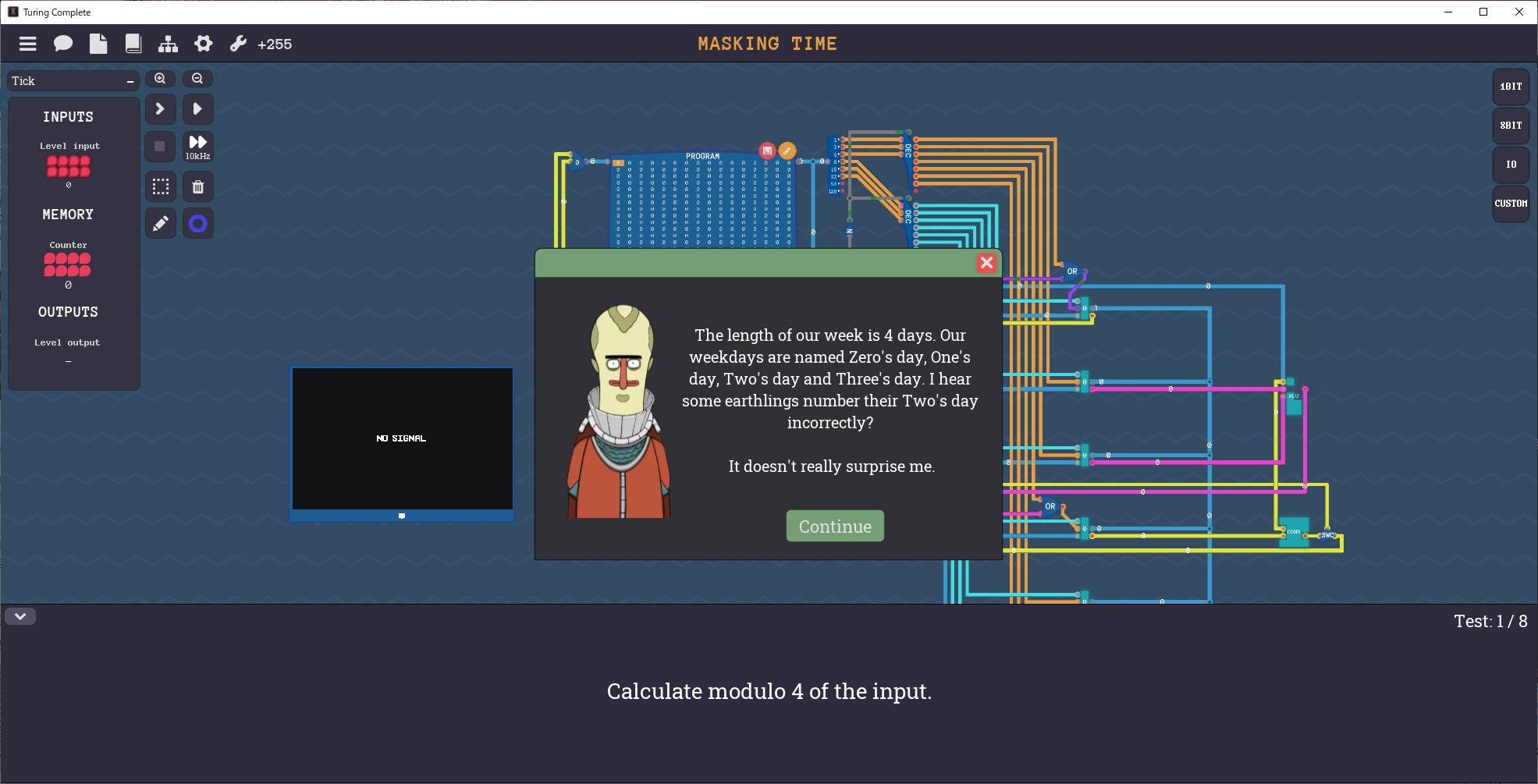
冒頭で提示されるメッセージは次の通りです。

The length of our week is 4 days. Our weekdays are named Zero’s day, One’s day, Two’s day and Three’s day. I hear some earthlings number their Two’s day incorrectly?
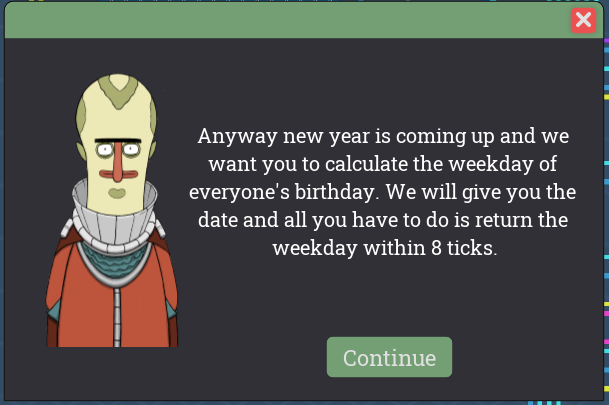
It doesn’t really surprise me.

Anyway new year is coming up and we want you to calculate the weekday of everyone’s birthday. We will give you the date and all you have to do is return the weekday within 8 ticks.

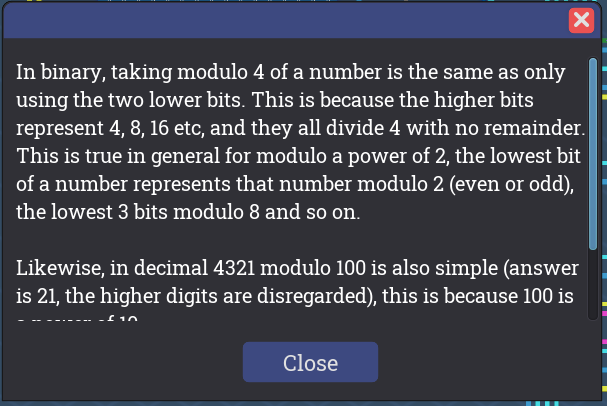
ヒントは次の通りです。

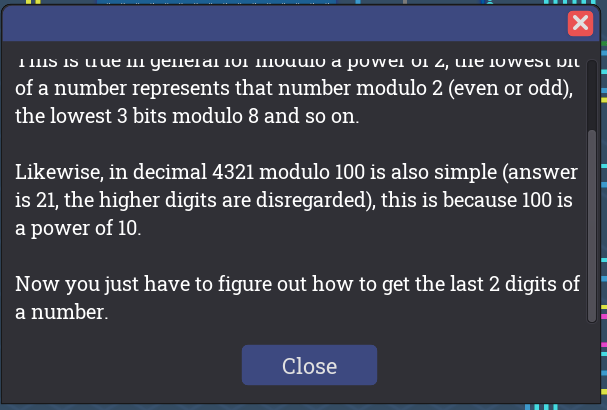
In binary, taking modulo 4 of a number is the same as only using the two lower bits. This is because the higher bits represent 4, 8, 16 etc, and they all divide 4 with no remainder. This is true in general for modulo a power of 2, the lowest bit of a number represents that number modulo 2 (even or odd), the lowest 3 bits modulo 8 and so on.

Likewise, in decimal 4321 modulo 100 is also simple (answer is 21, the higher digits are disregarded), this is because 100 is a power of 10.

Now you just have to figure out how to get the last 2 digits of a number.

余りを計算するには法（modulo）の概念を使うがわかりやすいとヒントをくれています。

10進数の場合は、法100（＝10²）を取れば下2桁（100で割った余り）が得られます。

対して、2進数の場合は、法4（＝2²）を取ると下位2ビット（4で割った余り）が得られます。

どうやって法4を計算するのかというのが、今ステージのテーマとなります。

Masking Timeステージを解く

1：2進数の法4を取るアルゴリズムを検討する

我々のCPUには除算機能がありませんので、ソフトウェアで実現しなければなりません。

2進数の法4を取る（4で割った余りを求める）処理をプログラムで実装するのです。

法演算（あるいは余りを求める計算）を実現するアプローチはいくつかあります。

①AND演算で指定の桁のビット列を取り出す。

②ビット列を左シフトして上位桁を取り除き、右シフトで調整する。

今回はアプローチ①を採用します。

2進数の法4を取るということは、対象ビット列（ここでは8ビット幅とする）に対して、0000 0011bでAND演算します。

ANDの定義からわかるように、後者のビット列における1の桁をそのまま抽出できます。対象ビット列側が0なら「0 AND 1⇒0」、1なら「1 AND 1⇒1」となるからです。

逆にいえば、後者のビット列における0の桁については、対象ビット列側が0でも1でも常に0になります。「0 AND 0⇒0」「1 AND 0⇒0」だからです。このように指定の桁を0に上書きすることをマスキング（マスク処理）といいます。

今回の例でいえば、上位6桁をマスク処理するわけです。

※ステージ名にも"Masking"とついているのはこのためです。

2：プログラムを実装する

実装したプログラムは次の通りです。コメントは、命令に対応するInstructionビット列です。

3				# 11b.マスキング用.
reg0_to_reg2	# 10 000 010b

in_to_reg1		# 10 110 001b
and				# 01 000 011b
reg3_to_out		# 10 011 110b

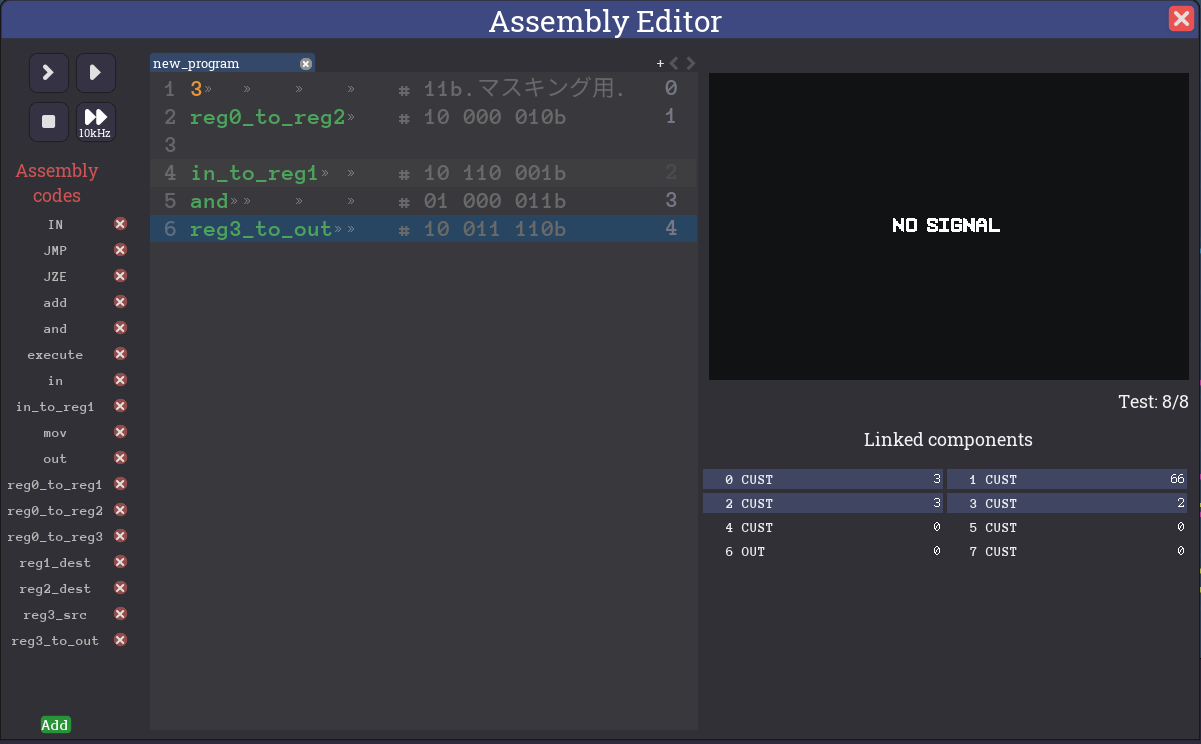
3：テストする

さまざまなテストパターンが入力されていき、すべてにパスすれば、ステージクリアとなります。