The Product of Nibbles【Turing Complete編】

2023年9月12日2023年12月5日

2進数値の乗算

A×Bという乗算（掛け算）であれば、Aを被乗数（multiplicand）、Bを乗数（multiplier）といいます。

・被乗数･･･乗数を掛けられる値。一般的に値は変わらない。

・乗数･･･被乗数に掛けて、結果である積（product）を求める数。

2の倍数を掛ける場合は左シフトするだけ

2ⁿを乗じる計算するには、2をn個掛け合わせてることになりますが、n回左シフトしても計算できます。

※2ⁿの除算は右シフトで実現できます。

それ以外の数を掛ける場合はどうするか

問題は2ⁿ以外を乗ずる場合です。

一番素朴な方法は、被乗数を乗数の回数だけ加算して積を求めるというアプローチです。C言語で実現すると次のような処理になります。multiplicandとmultiplierの数は与えられているものとします。

int product = 0;
int i;
for (i = 0; i < multiplier; i++) {
    product = product + multiplicand;
}

2進数でもこのアプローチは通用します。しかし、8ビットの乗算だと、最大で255回のループと加算処理が実行される可能性があります。つまり、このアプローチは、乗数の値が大きいときに、その分だけループの回数が増えて低速なのです。さらに、デジタル回路で実装するのは非常に困難です。

乗算の筆算のアルゴリズムは2進数でも通用する

各桁に対して基数を繰り返し被乗数に乗ずるのではなく、被乗数は乗数の各ビットに対して左シフトします。乗数ビットが1なら積に加算し、0なら積に加算せずに次の処理に移ります。

シフトと加算を使う方法なので、デジタル回路にも相性がよいといえます。

product = 0;
for (i = 0; i < log(multiplier); i++) {
    if ( (multiplier & 1) == 1) {  // LSビットがセットされていたら.
        product = product + multiplicand;  // 計算結果に加算する.
    }
    multiplier = multiplier >> 1;      // 乗数をシフトダウン.
    multiplicand = multiplicand << 1;  // 被乗数をシフトアップ.
}

ブースのアルゴリズム

（符号なし）4ビット乗算器

1ビット加算器から4ビット乗算器を構築する

$a_3 a_2 a_1 a_0 \times b_3 b_2 b_1 b_0 $

$=(a_3 a_2 a_1 a_0 \times b_0) + (a_3 a_2 a_1 a_0 \times b_1 \times 10b) + (a_3 a_2 a_1 a_0 \times b_1 \times 100b) +(a_3 a_2 a_1 a_0 \times b_1 \times 1000b) $　←(*)

[1]$a_3 a_2 a_1 a_0 \times b_0$の回路

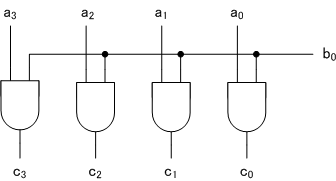
[2]$a_3 a_2 a_1 a_0 \times b_1 $の回路

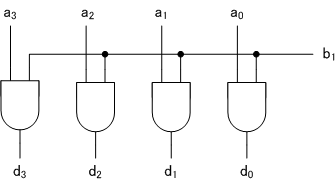
[3]$a_3 a_2 a_1 a_0 \times b_2 $の回路

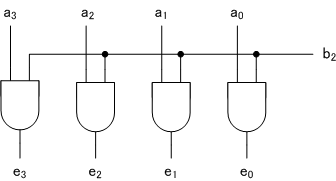
[4]$a_3 a_2 a_1 a_0 \times b_3 $の回路

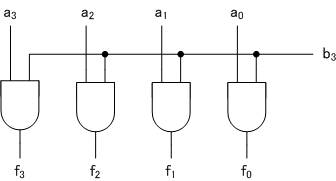
新しい変数を用いると、(*)式は次のように書き換えられます。

$c_3 c_2 c_1 c_0 +(d_3 d_2 d_1 d_0 \times 10b) +(e_3 e_2 e_1 e_0 \times 100b) +(f_3 f_2 f_1 f_0 \times 1000b) $

10b、100b、1000bを掛けるというのは、桁がずれていくことを意味します。

このことを考慮して、1ビット加算器を12個使えば、次の回路ができあがります。

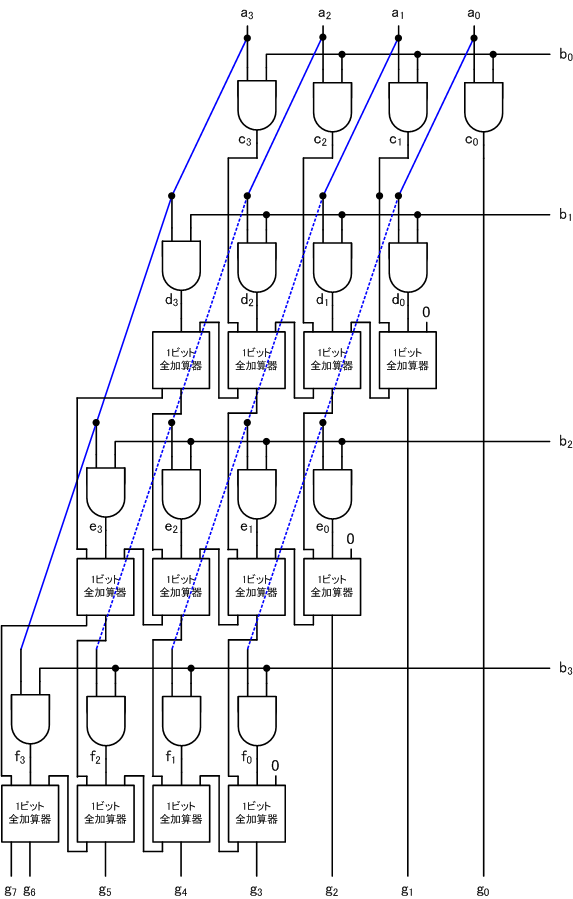
$a_3 a_2 a_1 a_0 \times b_3 b_2 b_1 b_0 = g_7 g_6 g_5 g_4 g_3 g_2 g_1 g_0$

4ビット加算器から4ビット乗算器を構築する

4ビット加算器を3つ使えば、次の回路に書き換えられます。

The Product of Nibblesステージ

The Product of Nibblesステージのゴールは、乗算回路を組むことです。

2つの4ビット列が入力として与えられたとき、その乗算結果は8ビットになります。

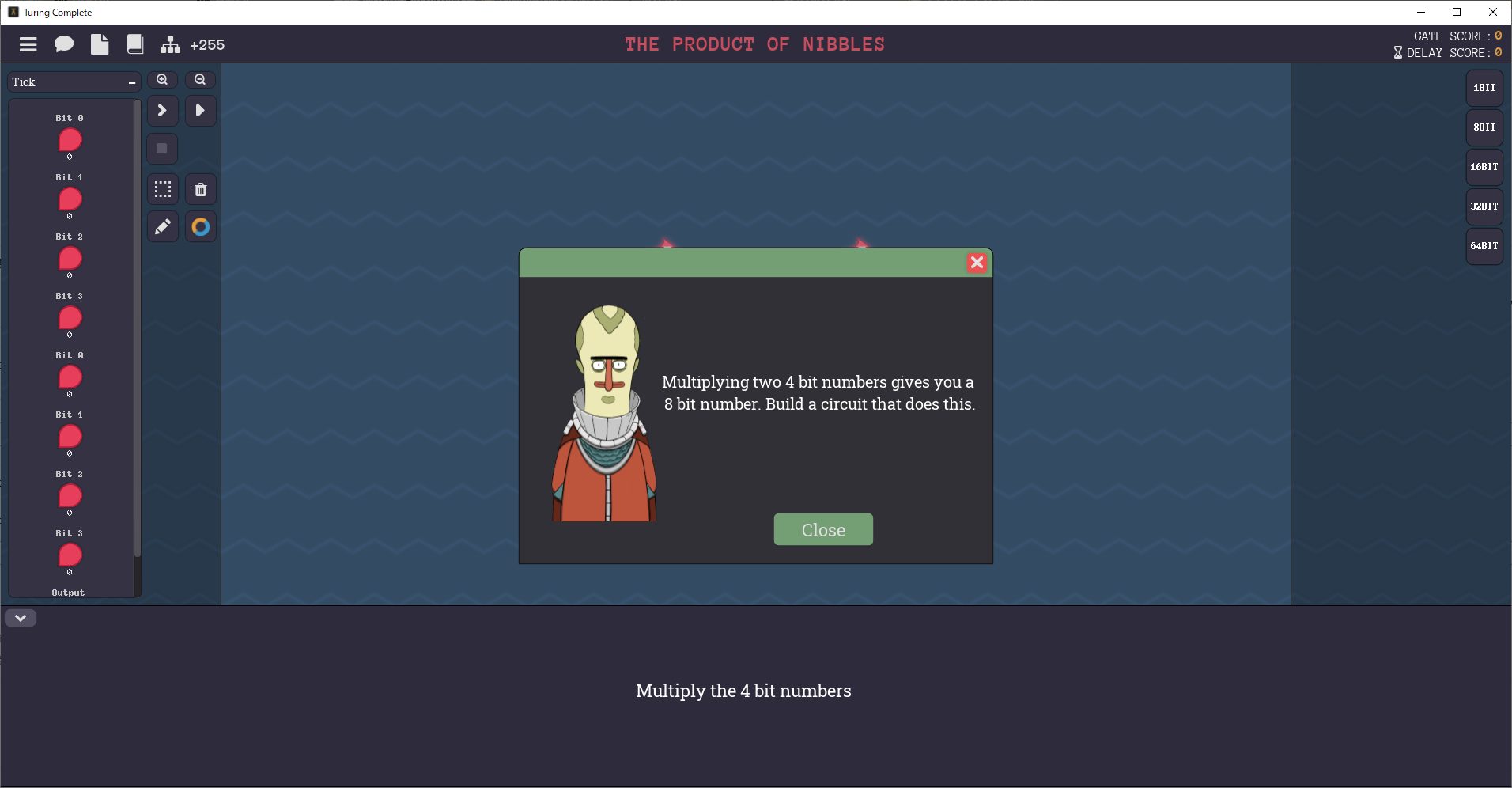
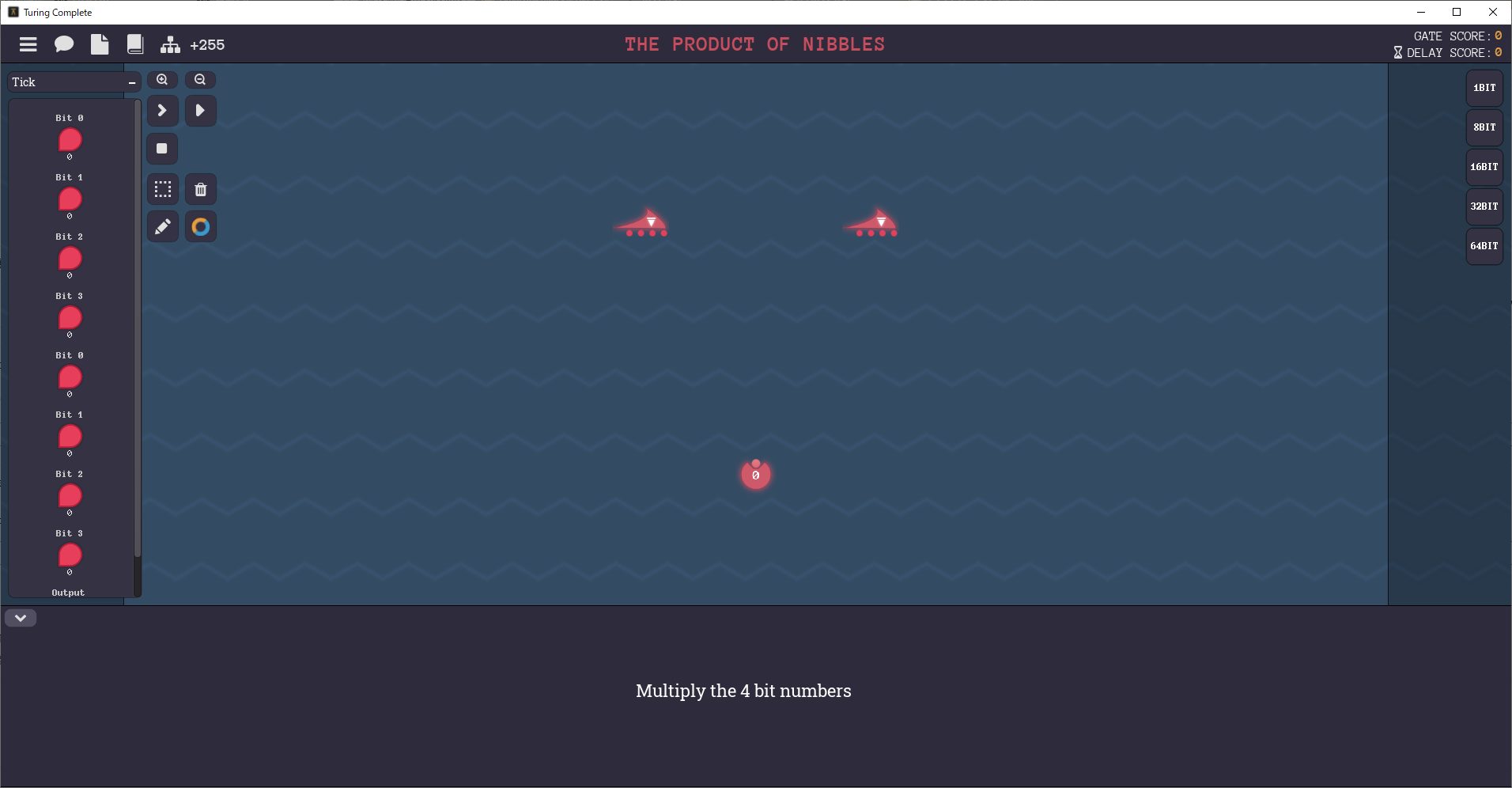
The Product of Nibblesステージを解く

1：入力端子と出力端子を確認する

キャンバス上に入力端子と出力端子が配置されています。

特に入力端子が2つあるので、被乗数と乗数がどちらに対応するか、ランプをON・OFFさせて確認しておきます。

2：乗算回路の設計方針を検討する

筆算のアプローチを見ると、可能性のある各乗算値に対して、すべての被乗数ビットを加算するように配線します。乗数ビットは、被乗数ビットのそれぞれに対してAND演算することで計算します。ANDを使えば、0のときに必ず0となるからです。もし乗算ビットがゼロなら、シフトアップした非常算ビットは加算器に渡されません。

よって、全加算器とAND回路を組み合わせれば実現できそうです。左にシフトするところは、回路上で1つずつ左シフトのようにずれていく回路を作ればよいのです。

シミュレーターでは、ANDコンポーネントとFull Adderコンポーネント（1ビット全加算器）を組み合わせて加算器を構築していきます。

3：回路を実装する

4ビット加算器があればよいのですが、シミュレーターには1ビット加算器と8ビット加算器しかありません。今回は1ビット加算器を使うことにします。

1ビット加算器であるFull Adderコンポーネントの入出力を再確認しておきましょう。Input 1～3があり、どこをCarry Inに使っても加算器の機能上問題ありません。ただし、使い方に統一性がないと回路が見づらくなるので、今回はInput 1をCarry Inとして扱うことにします。

検討の結果、回路を実装すると次のようになります。形が筆算のようになっていることがわかります。

被乗数が左側の入力端子（青色のワイヤー）、乗数が右側の入力端子（紫色のワイヤー）になります。

乗数から0のビットがくれば、そのラインはANDコンポーネントによって、すべて0000bとなり、ゼロを加算することになります。

一方、乗数から1のビットがくれば、1111bとAND演算することになるわけで、結果的に被乗数であるxxxxb（桁をずらした形で）加算します。

回路そのものより、きれいにワイヤリングするのが大変でした。

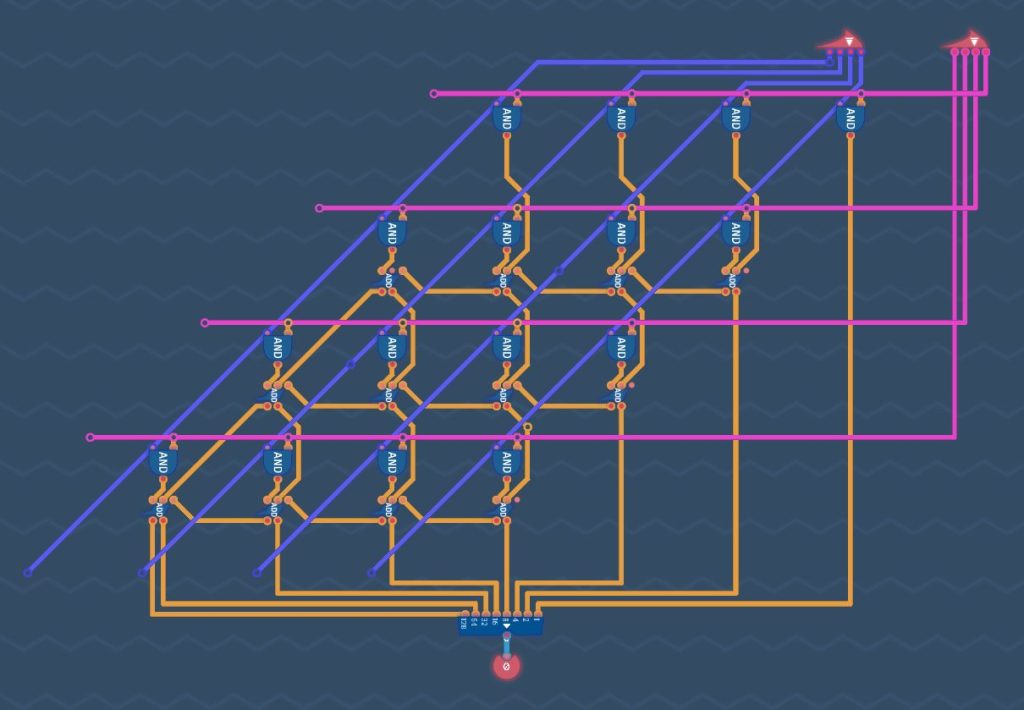
この回路の特徴として、4ビット同士の乗算の場合、16個のANDコンポーネント、12個^[1]1段目は不要のためです。のADDコンポーネントが必要になることが挙げられます。

加算器のキャリーアウトが確定したから隣の加算器のキャリーインに入ります。それが繰り返されます。左下の加算器の計算が確定するのは最後になります。つまり、計算が完了するのに遅延があるということです。

※nビットの場合、キャリーの伝搬段数が最悪3n-4段になります。今回は4ビットなので、最悪8段になります。

4：テストする

テストにパスすると、ステージクリアになります。

今回は4ビット乗算器（入力が4ビット）を実装しました、ステージクリアすると8ビット以上（バイト単位）の加算器まで拡張してくれます。

8 Bit Makerコンポーネントの力を借りる【別解】

乗算を実現するには「ずらして加算するが、乗数の桁が0なら加算しない」という筆算テクニックを活用できることを解説しました。

前述の回路はそれを愚直に実現した回路ですが、我々のシミュレーターには8 Bit Makerコンポーネントがあります。このコンポーネントの力を借りれば、より回路をすっきりさせられます。

ポイントは、4つの8 Bit Makerコンポーネントを用意し、入力の8つのピンのうち4つを使います。どこを使うのかは1つずつずらしていくわけです。

8 Bit Makerコンポーネントの出力を加算するかどうかは、乗数の各桁の値で判定します。

Addコンポーネント（8ビット全加算器）を使えば、8ビットのまま次々と加算できます。

以上を踏まえて、回路を実装すると次のようになります。

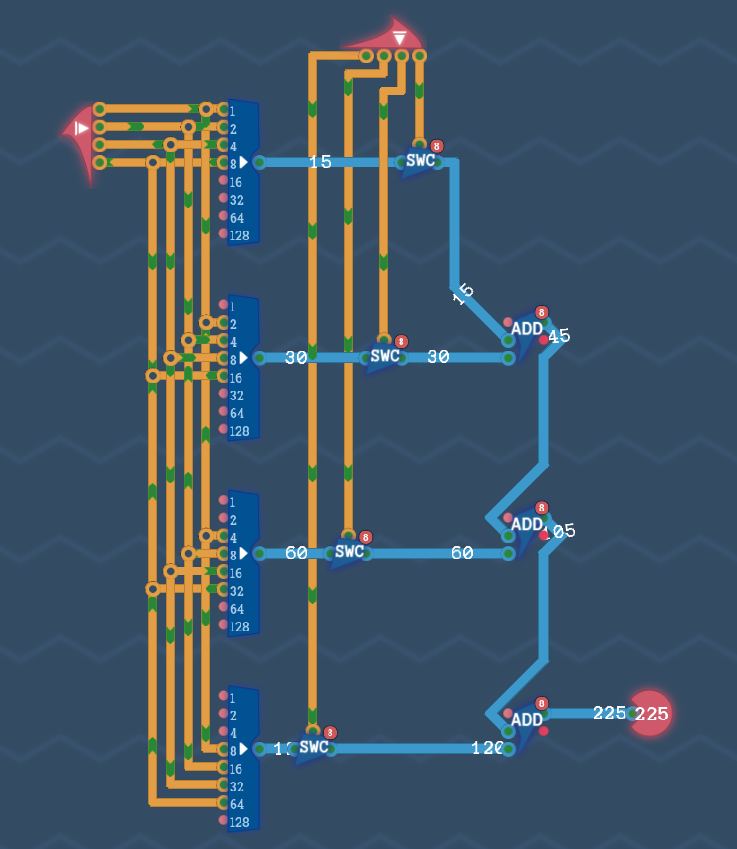
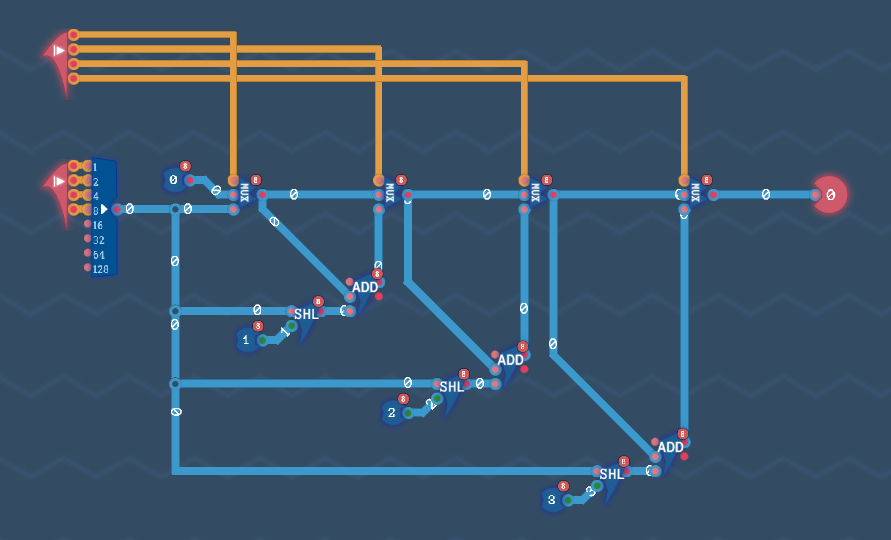
マルチプレクサーを活用する【別解2】