Add signed magnitude【NandGame編】
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
NandGameの符号つき整数
当該レベルにおいての符号つき整数は、sgとMで構成されるものとします。sgは符号、Mは符号なしの数を示します。
sg=0なら正、sg=1なら負と定義します。
例えば、「-2」という数は、sg=1、M=2となります。
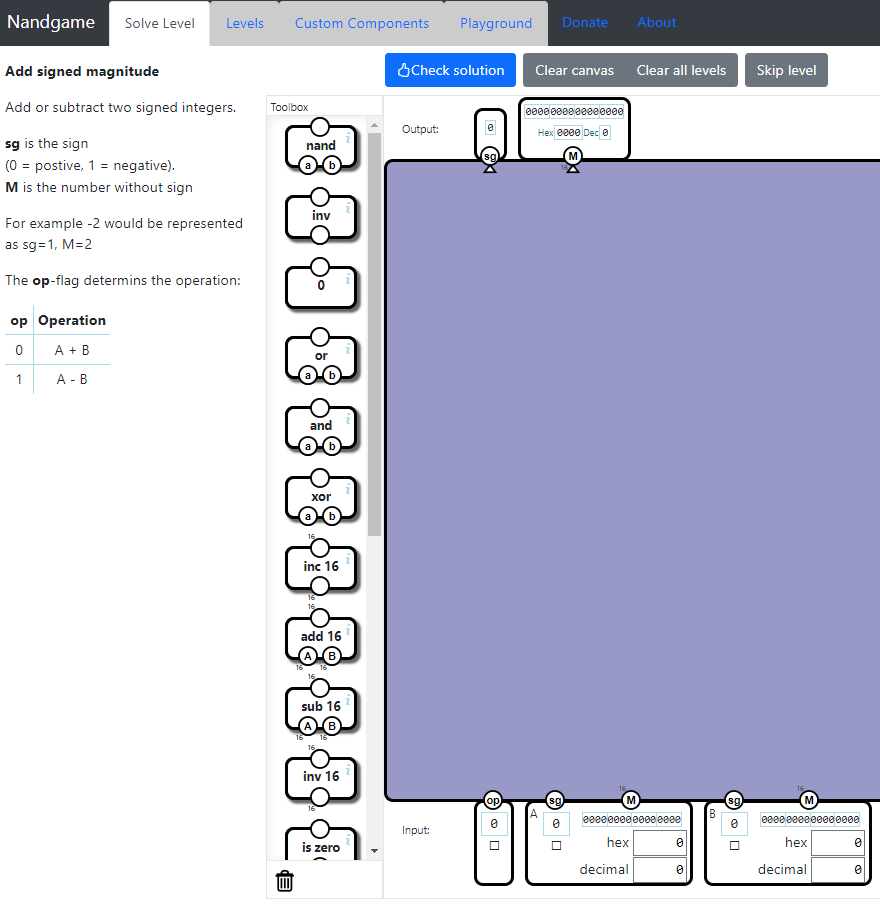
Add signed magnitudeレベル
Add signed magnitudeレベルのゴールは、2つの符号つき整数を加算または減算する回路を実装することです。
| 入力 | op | op(operation)フラグ。1ビット。 0なら加算(A+B)、1なら減算(A-B)。 |
| A | 1つ目の整数。 ・sg(sign):符号。0なら正、1なら負。例えば「-2」という数は、 ・M(magnitude):符号なしの数。 | |
| B | 2つ目の整数。 ・sg ・M | |
| 出力 | sg | 演算結果の符号。 |
| M | 演算結果の符号なしの数。 |
Add signed magnitudeレベルを解く
1:設計方針を検討する
正の数同士の加算・減算であれば簡単ですが、今回は正負が混在しています。2つの入力値があるので、次の4パターンに場合分けできます。
[1]Aが正の数、Bが正の数の場合
[2]Aが正の数、Bが負の数の場合
[3]Aが負の数、Bが正の数の場合
[4]Aが負の数、Bが負の数の場合
2:[1]のケースの加算回路を実装する
まずは加算回路から組んでいきます。
[1]のケースの加算については簡単です。入力のsgを無視して加算してしまいます。出力のsgに何もつなげなければ、0が出力され、結果も矛盾しません。
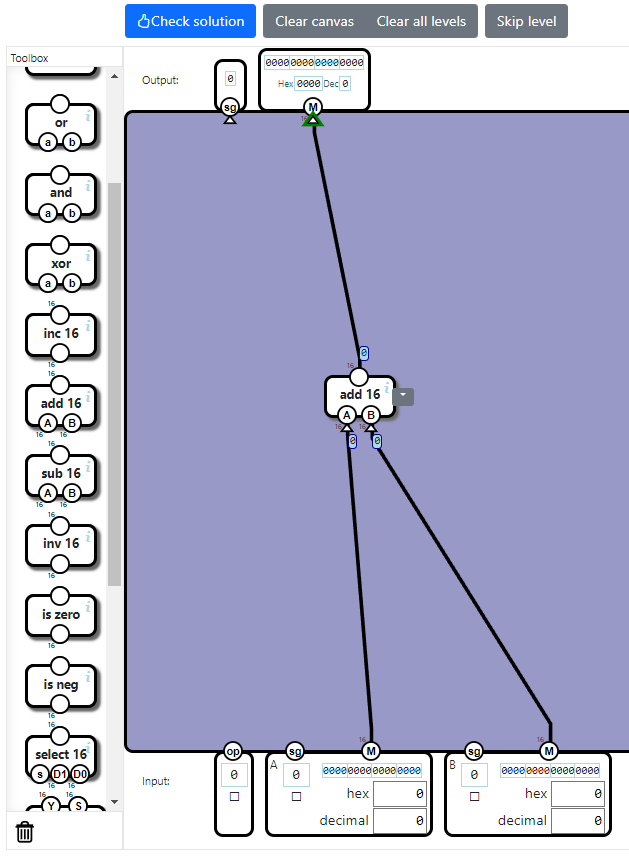
入力のopが0のときに加算結果を出力するので、select 16コンポーネントを配置しておきます。
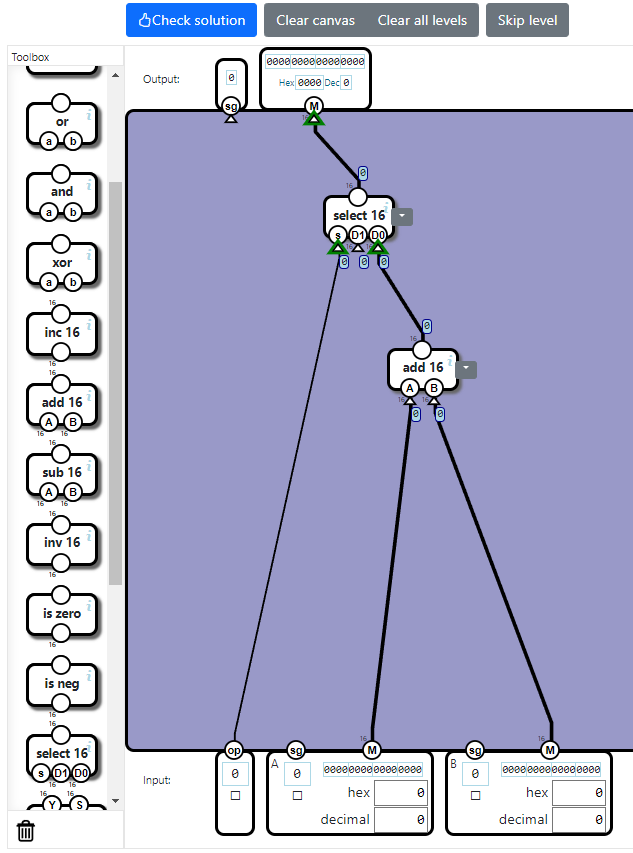
3:[4]のケースの加算回路を組み込む
既存の回路に追加する形で考えていきます。
Mの加算についてはそのままで問題ありません。
出力のsgは入力のsgになります。[1][4]のケースではAとBのどちらのsgも同一であるため、select 16コンポーネントのsピンは未入力でも問題ありません。これなら常にD0が選択され、Aのsgの値が出力されます。
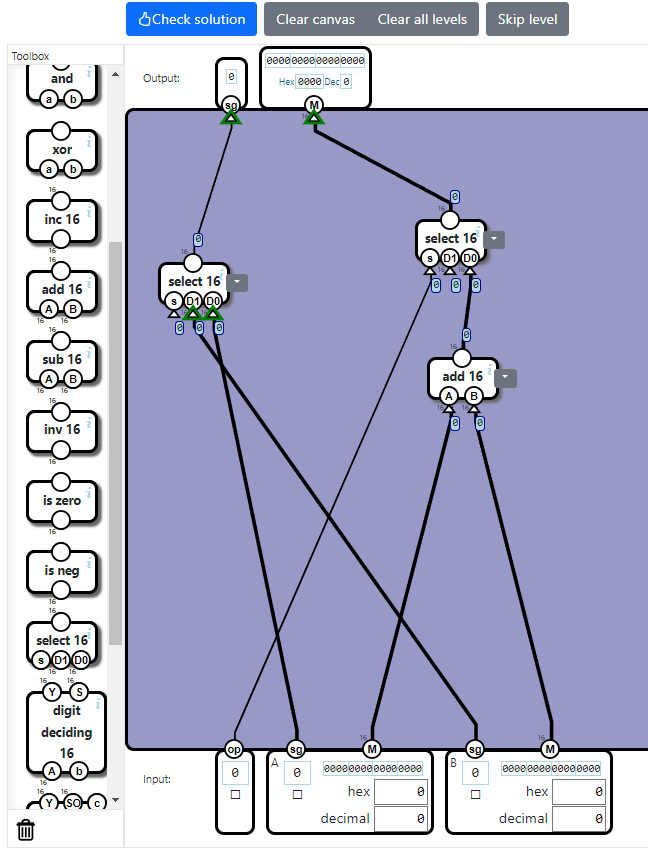
4:[2]のケースの加算回路を組み込む
正の数と負の数の加算なので、符号なしの数からすれば実質的に減算になります。引かれる値と引く値の大小によって、計算回路が逆転するので、次の3パターンに場合分けします。
※[3]のケースは、単純に[2]の処理を対称にすればよいと想像できます。
(i)(AのM)>(BのM)の場合
演算結果は正になるので、出力sg=0にならなければなりません。
出力Mは、(出力M)=(AのM)-(BのM)と計算します。
(ii)(AのM)=(BのM)の場合
演算結果はゼロになるので、出力sg=0でなければなりません(正に含めている)。
出力Mを計算するには、(出力M)=(AのM)-(BのM)でも、(出力M)=(BのM)-(AのM)でもどちらでも構いません。
(iii)(AのM)<(BのM)の場合
演算結果は負になるので、sg=1にならなければなりません。
出力Mは、(出力M)=(BのM)-(AのM)と計算します。
※入力の2つのMのうち大きい方を、減算の先に持ってきます。
ところで、各パターンの条件を「(AのM)-(BのM)」の形で言い換えると、次の2パターンに集約されます。
(a)(AのM)-(BのM)が負以外の場合・・・(i)と(ii)が該当する。
(b)(AのM)-(BのM)が負の場合・・・(iii)が該当する。
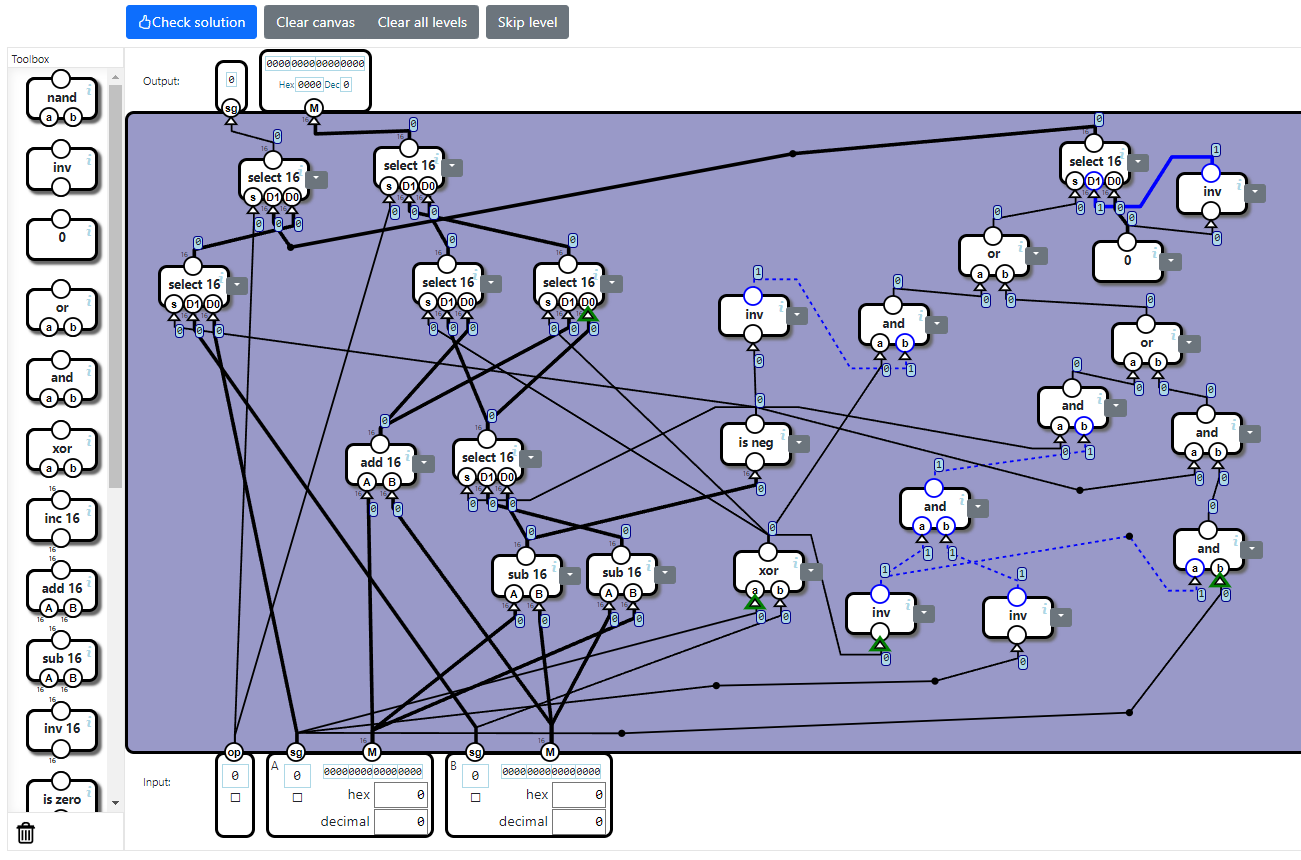
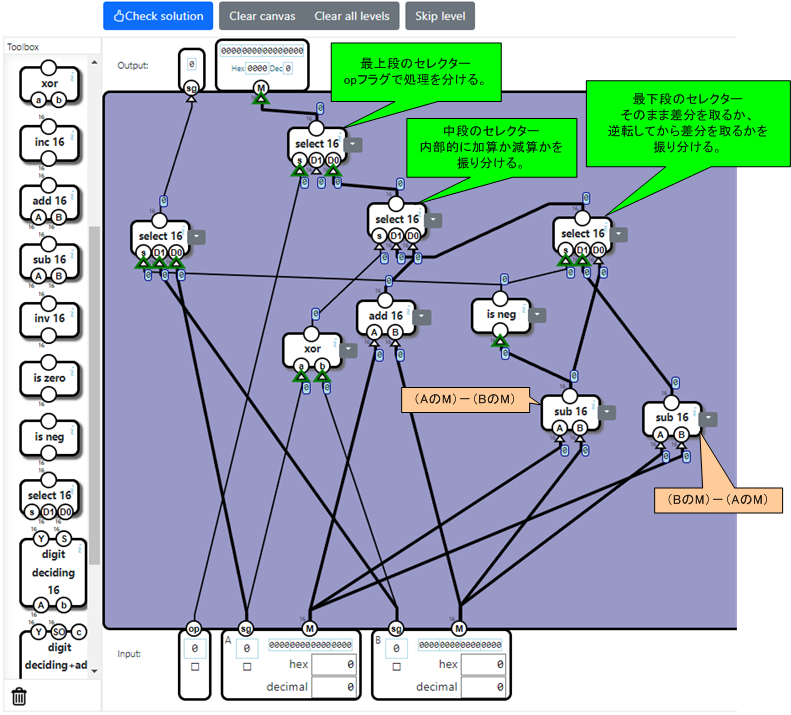
以上を踏まえて回路を組み込むと次のようになります。
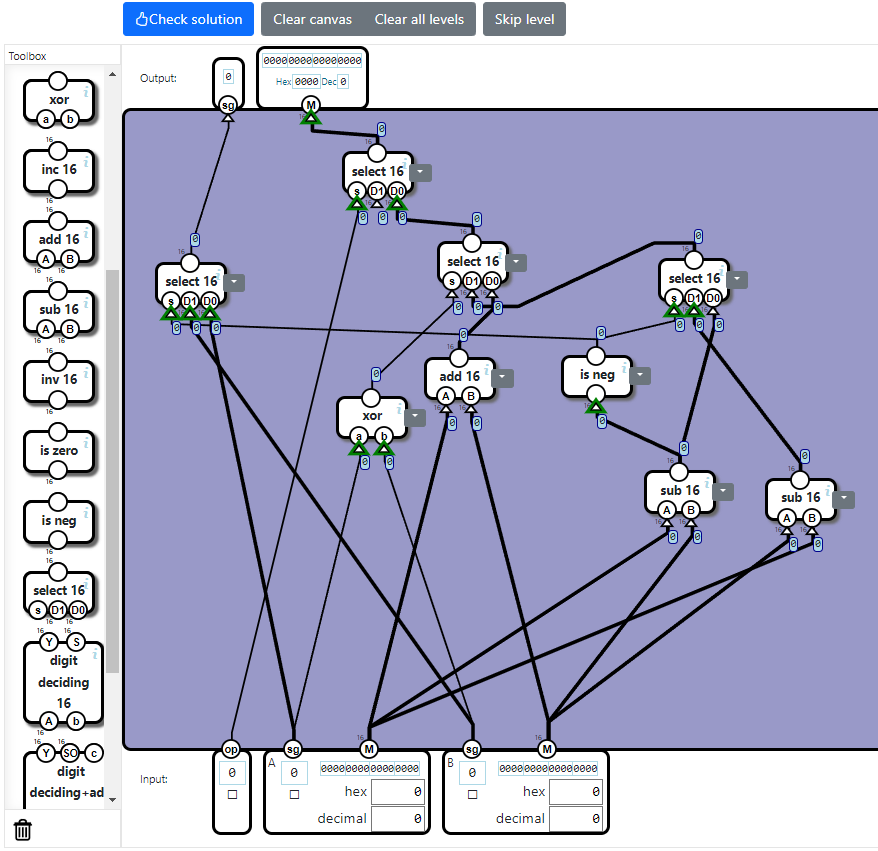
ところで、出力Mに連なるセレクター(select 16コンポーネント)が3段になっています。
・最上位(最終段)はopフラグでデータを振り分けるもの。
・中段はMの計算において加算([1][4])と減算([2][3])のどちらを使うのかを決めるためのもの。
・最下位(初段)は「(AのM)-(BのM)」と「(BのM)-(AのM)」のどちらの計算結果を決めるためのもの。
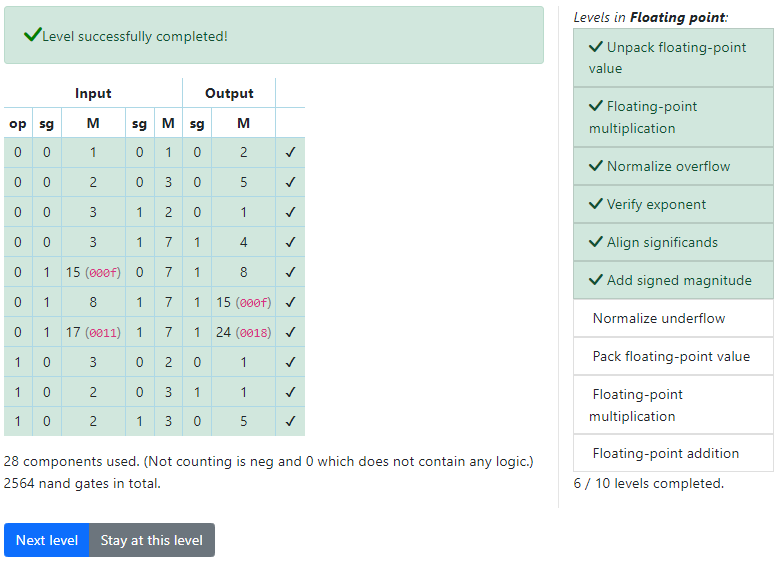
現時点でどこまでうまくいっているのか確認するために、用意されているテストパターンを試してみましょう。
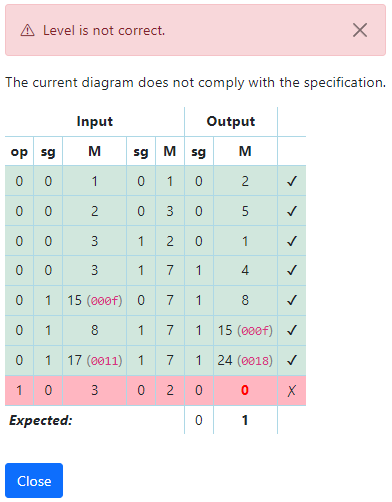
op=1のときに失敗するのは自明です。まだ回路を組んでいないためです。
なんとop=0のときはすべてのテストにパスしています。[1][2][4]に対応するテストはパスすることを期待していましたが、[3]に対応するテスト(表の5行目)もパスしてしまっています。
[2]の回路を組み込んだ時点で、[3]も解決していたことを示唆します。
実際に[3]のケースをトレースしてみましょう。[3]はAの負(Aのsgが1)、Bが正(Bのsgが0)のケースです。さらに、[2]のときと同様に次の3パターンに場合分けします。
(i)(AのM)>(BのM)の場合
sg=1、M=(AのM)-(BのM)になります。
(ii)(AのM)=(BのM)の場合
sg=0、M=(AのM)-(BのM)=(BのM)-(AのM)になります。
(iii)(AのM)<(BのM)の場合
sg=0、M=(BのM)-(AのM)になります。
Mの計算式については[2]とまったく同じであり、(i)と(iii)のsgだけが[2]と逆になっているだけです。
よって、Mの計算回路は[2]と[3]で共用できるということです。
(ii)のsgについてが気になるかもしれませんが、中段セレクターの制御フラグはXORゲートを通すので問題ありません。下段セレクター(Mの計算の振り分け処理)の制御フラグが逆になっとしても2つの入力はどちらも0(=M)になっているはずなので問題となりません。
5:減算処理を組み込む
場合分けについてはこれまでの議論どおりです。
[1′]Aが正かつBが正の場合、すなわち(Aのsg)=(Bのsg)=0の場合
[2′]Aが正かつBが負の場合、すなわち(Aのsg)=0かつ(Bのsg)=1の場合
[3′]Aが負かつBが正の場合、すなわち(Aのsg)=1かつ(Bのsg)=0の場合
[4′]Aが負かつBが負の場合、すなわち(Aのsg)=(Bのsg)=1の場合
一番簡単なのは、[2′]のパターンです。
(AのM)-(BのM)=正-負=正+正
よって、入力AとBのMは加算すればよいだけです。このとき、出力sg=0になります。
次に簡単なのは、[3′]のパターンです。
(AのM)-(AのB)=負-正=負+負
よって、入力AとBのMは加算したうえで、出力sg=1にすればよいのです。
続けて[1′]のパターンを見ます。
(AのM)-(BのM)=正-正
これはこのまま単純に考えられません。さらに大小関係で場合分けします。
(i)(AのM)>(BのM)のときは、出力sg=0、出力M=(AのM)-(BのM)
(ii)(AのM)=(BのM)のときは、出力sg=0、出力M=(AのM)-(BのM)=(BのM)-(AのM)=0
(iii)(AのM)<(BのM)のときは、出力sg=0、出力M=(BのM)-(AのM)
最後に[4′]のパターンを見ます。
(AのM)-(AのB)=負-負=負+正
同様に場合分けします。
(i)(AのM)>(BのM)のときは、出力sg=1、出力M=(AのM)-(BのM)
(ii)(AのM)=(BのM)のときは、出力sg=0、出力M=(AのM)-(BのM)=(BのM)-(AのM)=0
(iii)(AのM)<(BのM)のときは、出力sg=0、出力M=(BのM)-(AのM)
出力sgが[3′]と逆になっているだけで、出力Mは同じ計算で得られます。
今回(op=1)では、sgに注目すると次のようなパターン分けになります。
※このパターン分けでは、[1′][4′]は「2入力sgのXORの結果が1」のとき、[2′][3′]は「XORの結果が0」のときに対応することを考慮しています。
※AはAのM、BはBのMを示すものとします。
| ケース | 条件 | (XORの結果だけではsg=1を識別できない場合に用いる) 追加の条件 | 出力sg |
|---|---|---|---|
| a’ | XOR=1 かつ A-B<0 | - | 0 |
| b’ | XOR=1 かつ A-B>0 | - ※完全に識別OK | 1 |
| c’ | XOR=0 かつ A-B>0 | - | 0 |
| d’ | XOR=0 かつ A-B<0 | Aのsg=1 | 1 |
| e’ | XOR=0 かつ A-B>0 | Aのsg=1 | 1 |
| f’ | XOR=0 かつ A-B<0 | - | 0 |
sg=1になる条件をすべてANDで束ね、最終的にsg=1になる3パターンをORで束ねてしまえばよいのです。
加算のときのように単純にはいかないので、愚直に実装します。
得られた回路は次のとおりです。無事テストをパスします。
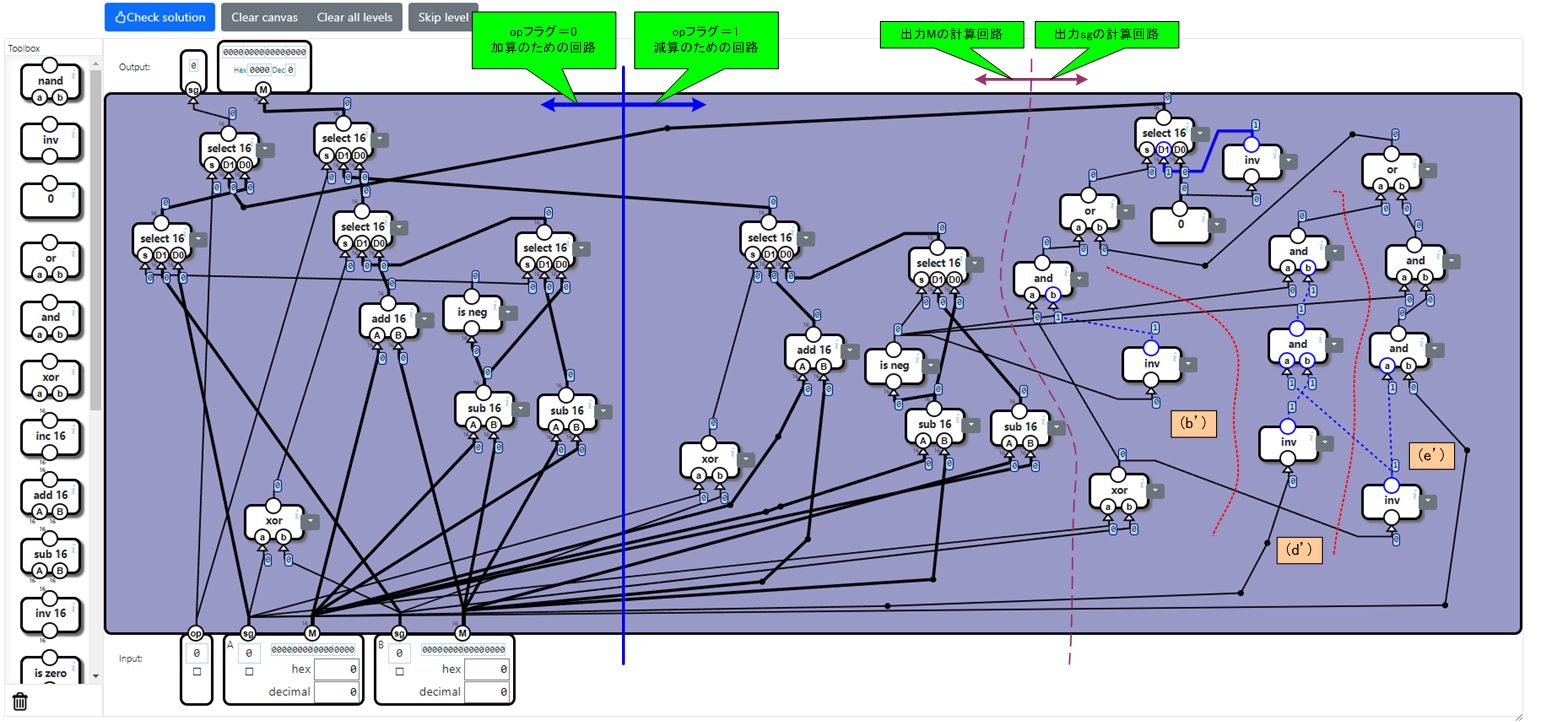
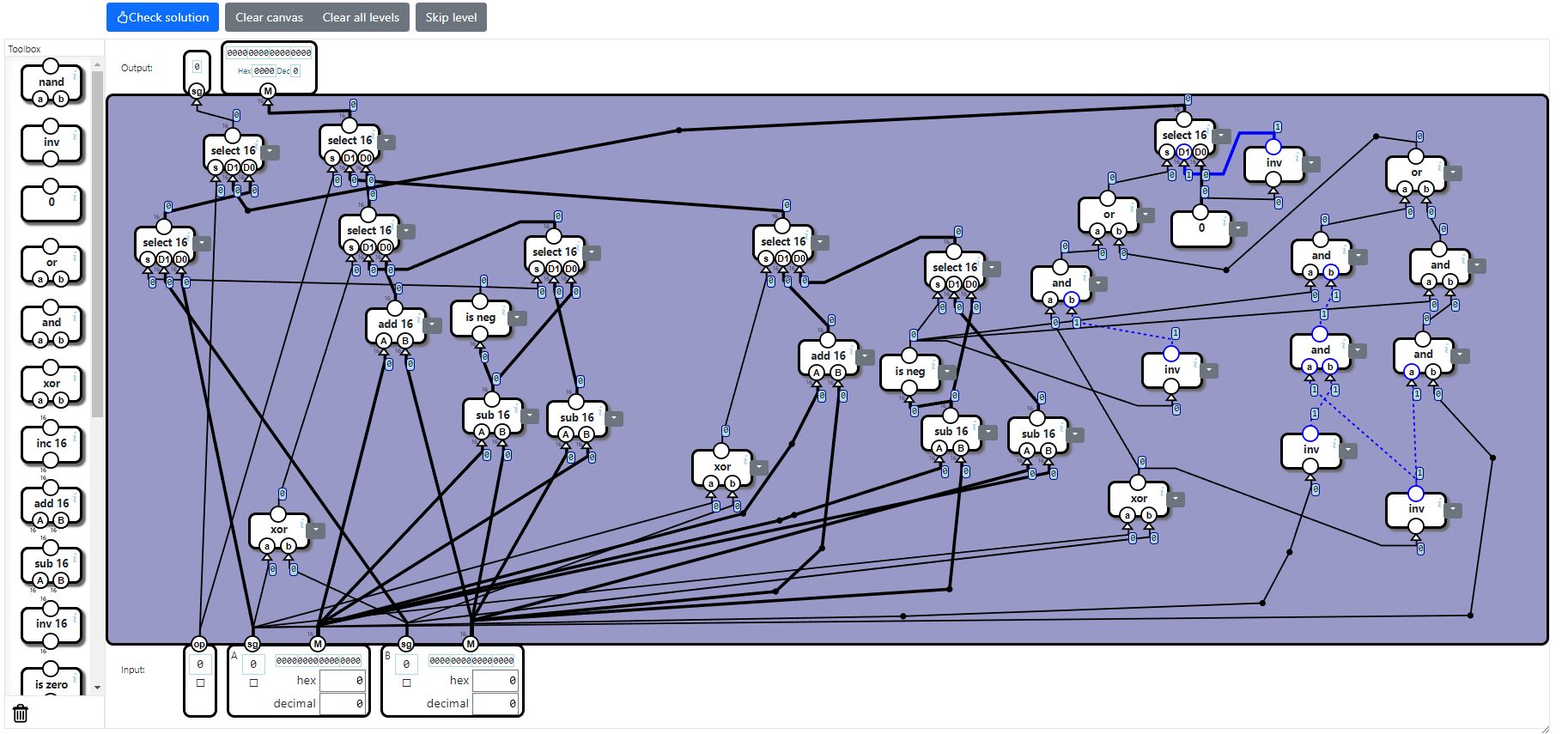
6:回路を最適化する
最終的にテストをパスする状態を維持しながら、重複するコンポーネントをカットしていきます。
最適化したらテストにパスすることを再度確認してください。