Saving Gracefully【Turing Complete編】
目次
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
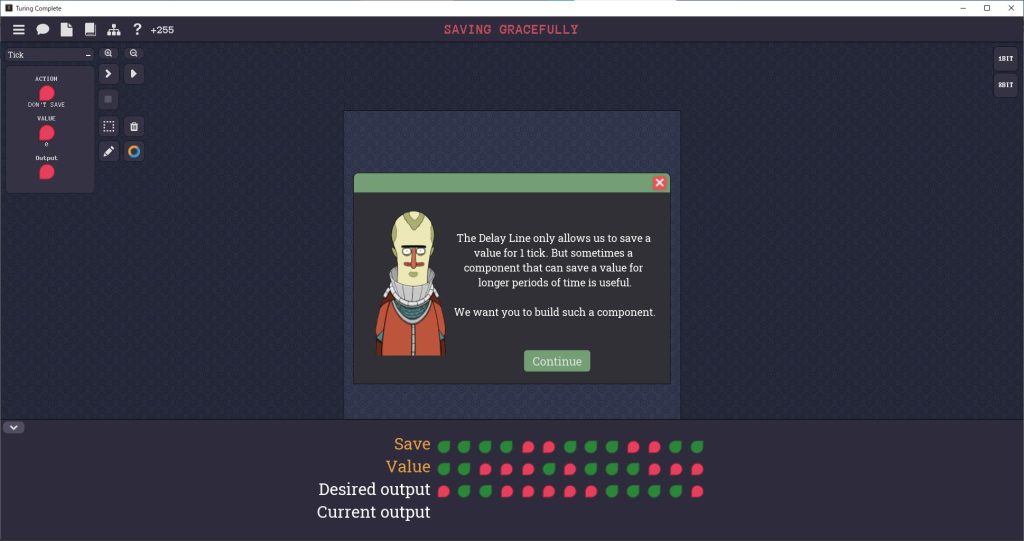
Saving Gracefullyステージ
Saving Gracefullyステージのゴールは、次の条件を満たす回路を組むことです。
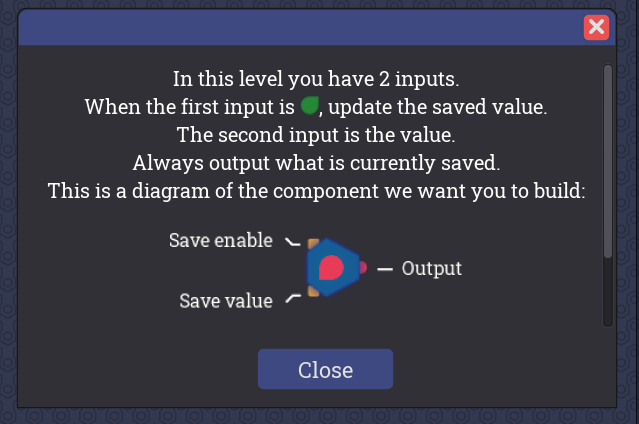
・2つの入力(SaveピンとValueピン)、1つの出力(Outピン)を備えている。すべて1ビット。
・1つ目の入力であるSaveピンはセーブ有効の制御用。ONならデータを保持する。
・2つ目の入力であるValueピンはデータ用。
・出力Outには、常に直近の保持データが出力される。
※回路は最後の値を覚えており、データが変わっても出力に影響しません。
順序回路は記憶回路に使える
順序回路とは、出力が「現在および過去の入力」によって決まる回路です。
過去の入力状態を出力に反映できるので、記憶回路(メモリー)として使えます。
※Turing Completeのシミュレーターでは1tickを通過することで時間の概念が生まれています。
NOTゲートだけで循環させた回路
1つのNOTゲートでは発振しない
1つのNOTゲートをつないだ回路を考えます。
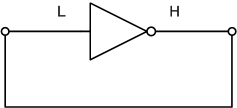
始めに入力端子をLレベル(0)にすれば、出力はHレベル(1)になります。
出力がTになれば、入力もTになり、次の瞬間には出力がLになります。
これが繰り返されて、出力端子が次々とHレベルとLレベルを繰り返し(発振)そうですが、実際にはそうなりません。
FからHに切り替わる時間と回路の遅延時間がほぼ等しいため発振しないのです。
2つのNOTゲートだと2つの状態で安定できる
2つのNOTゲートをつないだ回路を考えます。
※フリップフロップの原型になります。
このとき、2つの状態で安定します。当然ながら発振はしません。
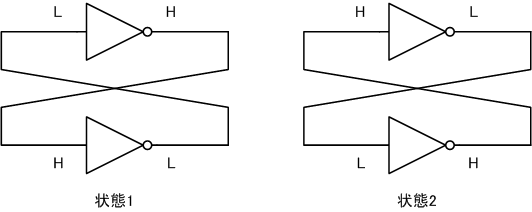
入力信号がなくても出力状態を保持できているので、記憶回路の一種です。
3つのNOTゲートだと発振する
ところが、3つのNOTゲートをつないだ回路だと発振します。
2つのNOTゲートによって入出力が打ち消し合いますが、遅延が発生することで発振するのです。
※発振したとしても、高速すぎて素子を痛める可能性はあります。
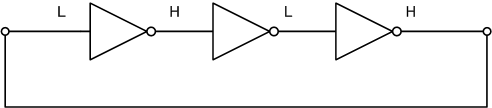
発振器については本テーマではないので、これ以上はここでは触れません。
もっともシンプルな自己保持回路
一度変化した状態を保持し続けられる回路を自己保持回路といいます。
ここではもっとも単純な自己保持回路として、一回プッシュボタンでONにしたら、ランプが点灯したままになる回路を考えます。

OUTPUTの信号がORの片方の入力にフィードバックされています。
INPUTが一回でもHighになると、以降OUTPUTがHighになり、Lowに戻りません。
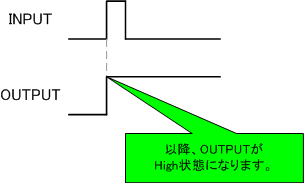
回路全体で信号がどうなっているのかをトレースしてみます。
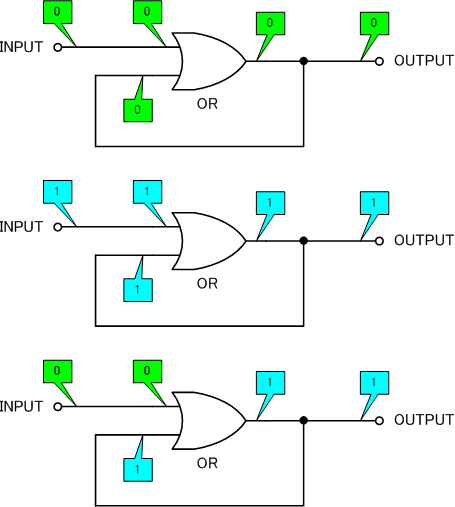
きちんと1がフィードバックされていて、一度ORゲートの出力が1になると、それが維持されています。
リセット機能を持つ自己保持回路
前述の自己保持回路は一度1を記憶してしまうと0に戻せません。これでは実用的ではないので、記憶した1を0に戻す仕組み、すなわちリセット機能が欲しいところです。
NOTゲートとANDゲートを追加するだけで実現できます。
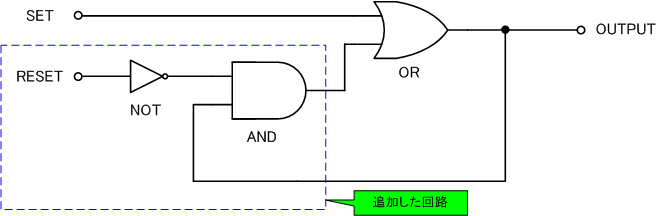
これをRSフリップフロップ回路といいます。
この回路の挙動をトレースしてみます。
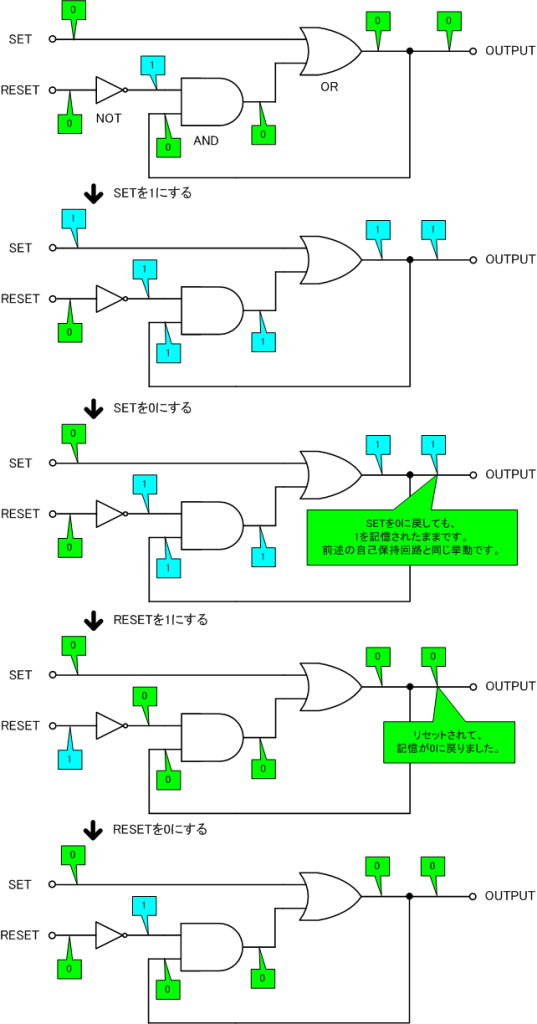
RSフリップフロップ回路では、1ビットを記憶するためのもので、SETとRESETはそれぞれ記憶とリセットを担当します。
そのため、SET信号とRESET信号が両方とも同時に1になることを想定していません。
※そのときの出力は不定であり、禁止と考えます。
信号を時間軸で現すと、次の波形が得られます。

2つのNORゲートによる記憶回路
ここからは別の論理ゲートを用いて考察し直します。
2つのNORゲート、2つのスイッチ、1つの電球を使って、次のように組んだ回路を考えます。
ここでは少しでも理解の助けになるように、冗長化もしれませんがあえてスイッチや電球を描いています。
一般的な技術書ではスイッチや電球を登場しない回路で説明されていますが、大好きな書籍『CODE』に倣いました。『CODE』P.200-の解説に対応します。
※ここではNORゲートを使いましたが、NANDゲートでも似た議論ができます。
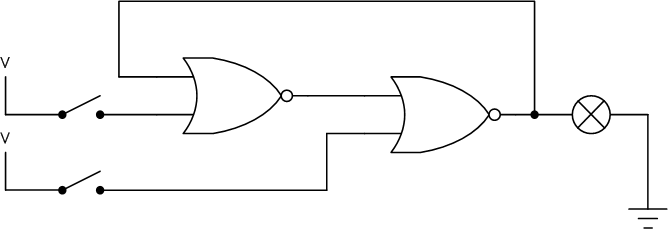
右のNORゲートの出力が、左のNORゲートの入力に回り込んでいます。
復習としてNORゲートの真理値表を載せておきます[1]ORのNOTと考えて、即座に真理値表を書けるようになっておくとよいでしょう。。この表を見ながら、スイッチをON・OFFした際の電球の点灯具合を調べましょう。
| A | B | OR(A, B) | NOR(A, B) (=NOT(OR(A, B)) |
|---|---|---|---|
| L | L | L | H |
| L | H | H | L |
| H | L | H | L |
| H | H | H | L |
初期状態は両方のスイッチがOFFです。電球は消灯しているので、左のNORゲートの上の入力はLになります。
Hになっているワイヤーを青色にします。
上のスイッチを操作する
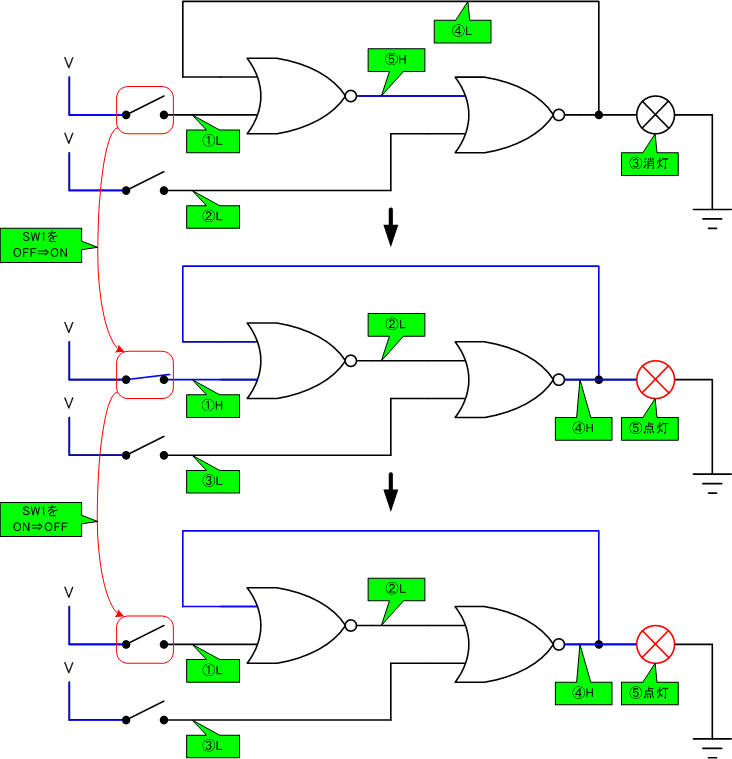
SW1をOFF⇒ONにしたとき、NORゲートの入力の1つがHです。NORゲートの定義より、入力が1つでもHなら、出力は常にLになります。その結果、電球が点灯します。
次にSW1をON⇒OFFに戻します。すると電球が点灯したままです。
両方のスイッチがOFFで、最初と同じ回路なのに、電球が点灯しています。『CODE』ではこの現象を「スイッチを切ったときに魔法が起こる」と称しています。
下のスイッチを操作する
今度は下のスイッチに注目します。
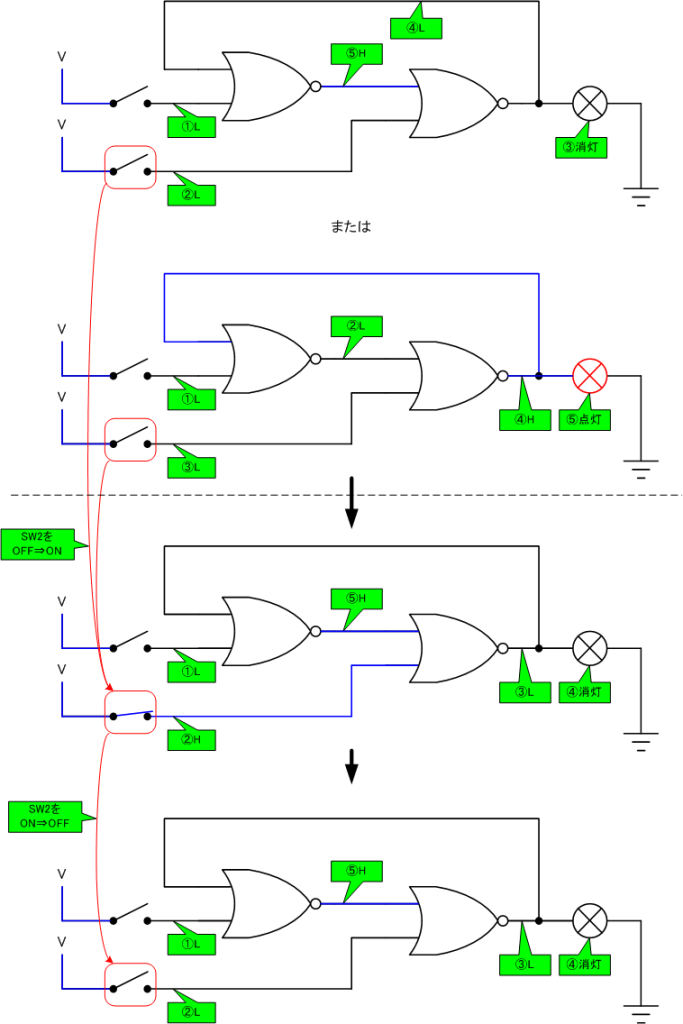
最初は電球が消灯・点灯のどちらかの状態になっています。
SW2をOFFからONにすると、右側のNORゲートの入力の1つがHになるので、出力はLになります。結果的に、電球は消灯します。
SW2をONからOFFに戻しても、電球は消灯したままです。
まとめ
[1]SW1をON⇒電球が点灯
続けてSW1をOFFにしても、電球は点灯したままです。
[2]SW2をON⇒電球が消灯
続けてSW2をOFFにしても、電球は消灯したままです。
両方のスイッチがOFFなのに、電球が点灯するときと消灯するときがありました。
これは両方のスイッチがOFFのときに、2つの安定状態を持つといえます。
このような回路をフリップフロップ(flip flop、FF)といいます。
フリップフロップは情報を保持する
フリップフロップは情報を保持、すなわち記憶します。
上記で示したNORゲートを使ったフリップフロップは、どちらのスイッチが最後にOFFになったのか(閉じられたか)を記憶しているといえます。
電球が点灯していたら、最後にOFFになったのは上のスイッチ(SW1)、消灯していたら最後にOFFになったのは下のスイッチ(SW2)と判断できるのです。
RSフリップフロップ
フリップフロップにはさまざまなタイプがあります。
これまでに示した2つのNORゲートを構成したフリップフロップはもっとも単純なタイプであり、RSフリップフロップと呼ばれます。
RSフリップフロップは、2つの安定状態を保持し、それを容易に制御できる回路です。
NORゲートをたすき掛けのようにして対称的に配置すると、次のようになります。
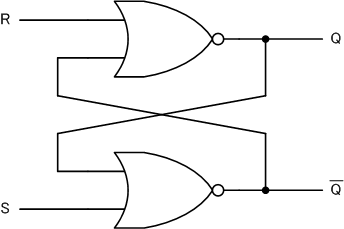
電球に使った出力はQに対応します。 ̄Qは「キューバー」と発音しますが、Qの反転値になります。
2つの入力RとSは、リセット(reset)とセット(set)に由来します。
真理値表
SがHのとき(前の説明ではSW1をONにすることに対応)、QはH、 ̄QはLになります。
RがHのとき(前の説明ではSW2をONにすることに対応)、QはL、 ̄QはHになります。
SとRが両方Lのとき、出力はRとSのうちどちらかが最後にQに行われたかを示します。
以上の結果とまとめると、次の真理値表が得られます。
| S | R | Q |  ̄Q |
|---|---|---|---|
| L | L | Q |  ̄Q |
| L | H | L | H |
| H | L | H | L |
| H | H | 不可 | 不可 |
SとRが両方ともLのとき、出力がQと ̄Qになっています。これはQと ̄Qは、SとRが両方Lになる前の値のまま出あることを意味します。
SとRが両方ともHになる状況は許されません。なぜなら、もし入力が両方ともHだと、出力も両方ともLになってしまい、Qと ̄Qが反対であることに矛盾します。
よって、RSフリップフロップを使う回路を設計する際には、SとRが両方Hになる状況を避けなければなりません。
ブロック図

信号を記憶する回路が欲しい
RSフリップフロップは、2つの入力のうちどちらが最後に電圧を持っていたかを覚えていました。これは興味深い回路ですが、もっと役立つものは、特定の信号が特定の時点でLだったのかHだったのかを覚えている回路です。
そのような回路を作る前に、期待する挙動について考えます。
入力は2つあり、その1つはデータと呼ぶことにします。もう1つをビット保持と呼ぶことにします。これはセーブすることを指示する事に対応します。
通常ビット保持信号はLであり、この場合はデータ信号(入力であるデータからくるビット値)は回路に何も影響を与えません。
ビット保持信号がHのとき、回路はデータ信号の値をそのまま反映します。
そして、ビット保持信号がLに戻ると、その時点で回路はデータ信号の最後の値を覚えています(出力も記憶している値)。入力であるデータ信号が変化しても、もう回路に影響はしません。
上記の挙動を実現する回路は、次の真理値表になります。
| データ | ビット保持 | 出力Q |
|---|---|---|
| L | L | Q |
| L | H | L |
| H | L | Q |
| H | H | H |
真理値表(ヘッダーは除外)の2行目と4行目に注目してください。ビット保持信号がHのときです。このときは出力Qはデータ入力と同じ値です。
1行目と3行目は、ビット保持信号がLのときであり、出力Qは前と同じ値になります。このとき、出力Qはデータ入力の値にかかわらずに同じであることに注意してください。
上記の真理値表は次のように簡略化できます。
| データ | ビット保持 | 出力Q |
|---|---|---|
| L | H | L |
| H | H | H |
| X | L | Q |
このXは何でもよいことを意味します。すなわち、ビット保持の入力がLなら、データの入力値にかかわらず、出力Qは前と変わりません。
RSフリップフロップからレベルトリガー型のDフリップフロップを作る
既存のRSフリップフロップに、2つのANDゲートを追加した回路を考えます。
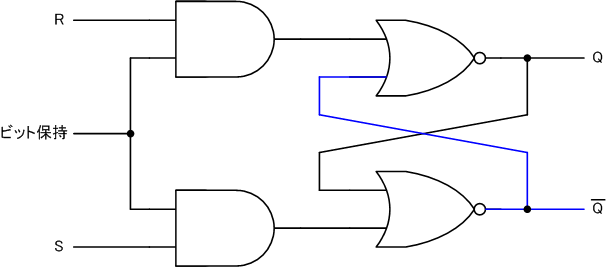
ANDゲートの出力がHになるのは、両方の入力がHのときだけです。この図では、ANDゲートの出力はLであり、後段にLとLが渡されます。禁止事項のHとHを渡していないので問題ありません。
このとき、出力QはL、 ̄QはHになります。
ビット保持信号がLである限り、RやSがHになっても、出力Qに影響を与えません。
ビット保持信号がHのときのみ、この回路は通常のRSフリップフロップと同様に動作します。
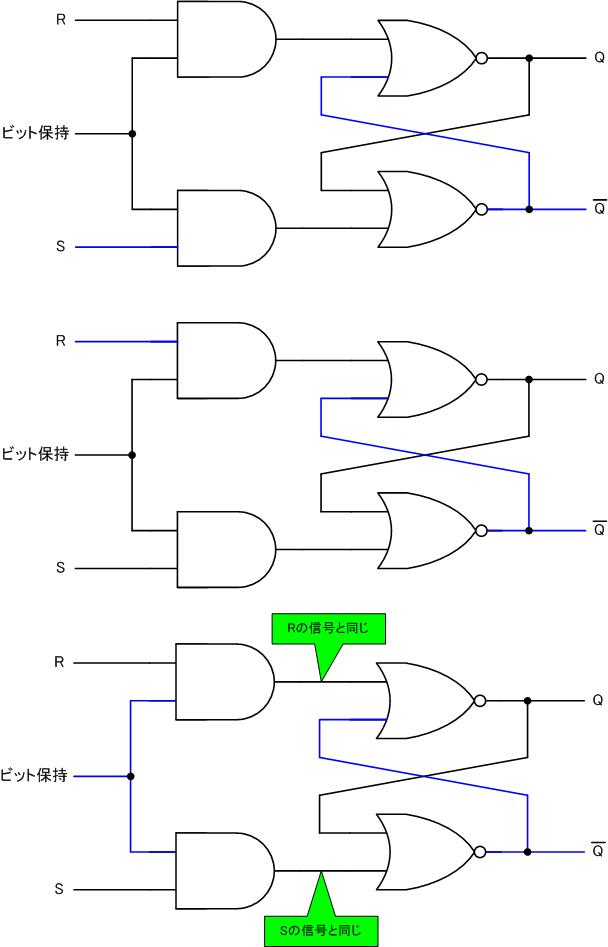
次に、入力を3つから2つにすることを目標にします。
ビット保持はそのまま使います。RとSの入力をうまく統合して、データにできればよいのです。
そのとき留意すべきことは次の通りです。
・①RSフリップフロップの真理値表において、SとRがHになるのは禁止されていたので、これを避ける。
・②SとRがLになる場合、単に出力が変わらないことである。
①については「SがT」なら「RがL」、「SがL」なら「RがH」に強制できる仕組みにすればよいのです。そこには、データ信号をセット信号とし、データ信号を反転したものをリセット信号にします。
②については簡単に達成できます。この回路でビット保持をLにするだけです。
回路は次のようになります。
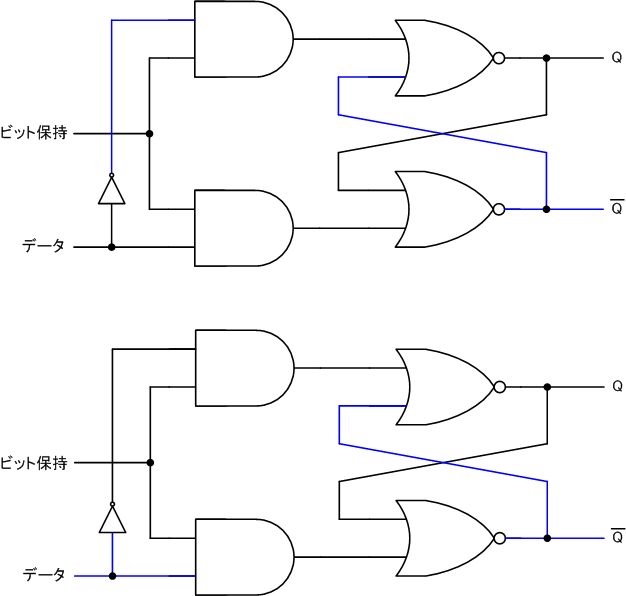
2つの図がありますが、どちらも同じ回路です。データ信号がLかHかの違いです。いずれにしても、ビット保持信号がLである限り、データ信号の入力は回路に影響を与えていません。
対して、データ信号が1のときは、次のように回路はデータ信号の入力値をそのまま反映します。このとき、出力Qはデータ信号の入力と同じです。
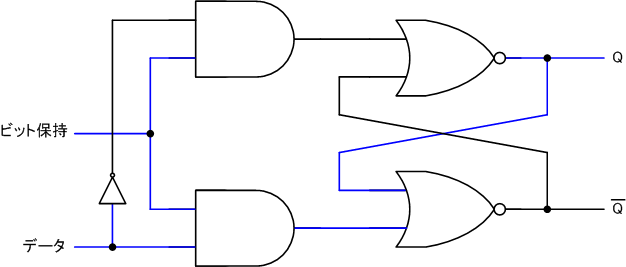
ここで、ビット保持信号をLに戻したとします。このとき、回路はデータ信号がどう変わっても、ビット保持信号が最後にHだったときのデータ信号の値を覚えています。データ信号をLにしても回路には影響を与えていませんし、出力も変化しません。
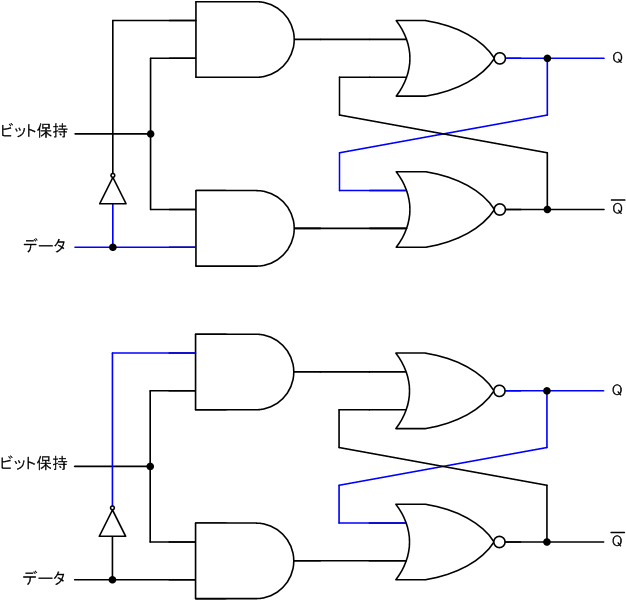
最終的にできた、この回路をレベルトリガー型のDタイプフリップフロップと呼びます。
・「D」はデータを意味します。
・「レベルトリガー」は、ビット保持信号の入力が「L⇒H」のときに、データ信号の入力値を記憶するからです。
※入力がビット保持ではなく、クロック信号の場合は、レベルトリガー型のDタイプラッチと呼びます。
Saving Gracefullyステージを解く
Inputは2ビットですが、上のInput 1がセーブ制御用、下のInput2がデータ用です。
Input 1がOFFならDon’t save、ONならSaveを意味します。

RSフリップフロップを改造してDラッチを構成する【解答】
シミュレーター上にレベルトリガー型のDタイプフリップフロップを組みます。
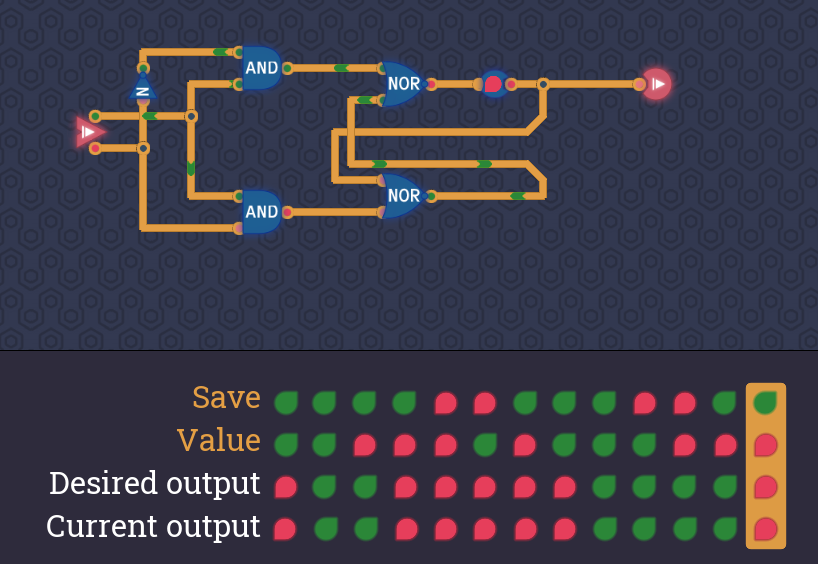
クリアすると1 Bit memoryコンポーネントがアンロックします。
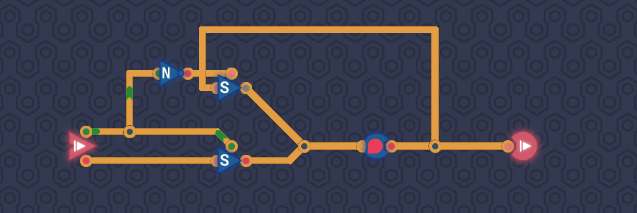
Switchコンポーネントを利用して組む【別解】
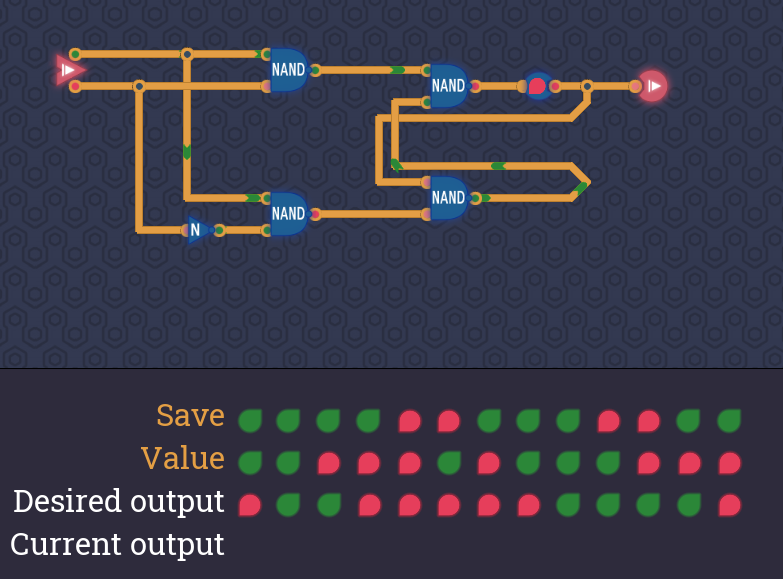
NAND回路をたくさん使う【別解2】
References
| ↑1 | ORのNOTと考えて、即座に真理値表を書けるようになっておくとよいでしょう。 |
|---|