Basic Logic【Turing Complete編】

2023年8月14日2023年9月15日

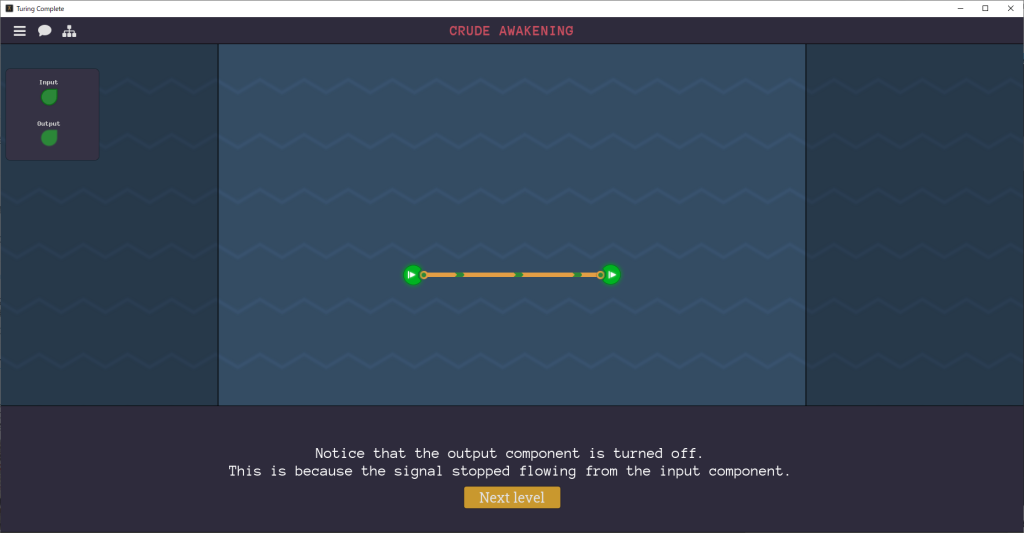
Crude Awakeningステージ

基本操作の説明です。

左上のINPUTをクリックするとON・OFFを切り替えられます。

それと同時に中央の画面の「＞」（入力）の色が緑色と赤色に交互に切り替わります。

・緑色＝電気が流れている＝ON

・赤色＝電気が流れていない＝OFF

※Turing CompleteではON・OFFと表現しているところは、T（True）・F（False）、1・0、H（High）・L（Low）と対応するものとします。

NAND Gateステージ

NANDゲートの動作を確認します。

Turing Completeにおいて最初にNANDゲートが取り上げられているのは、NANDゲートがあれば他のゲートを作れるからです。

NANDゲートの真理値表

次はNANDゲートの真理値表になります。a,bが入力、zが出力です。

a	b	z (=NAND(a,b))
0	0	1
0	1	1
1	0	1
1	1	0

Turing CompleteでNANDゲートに慣れる

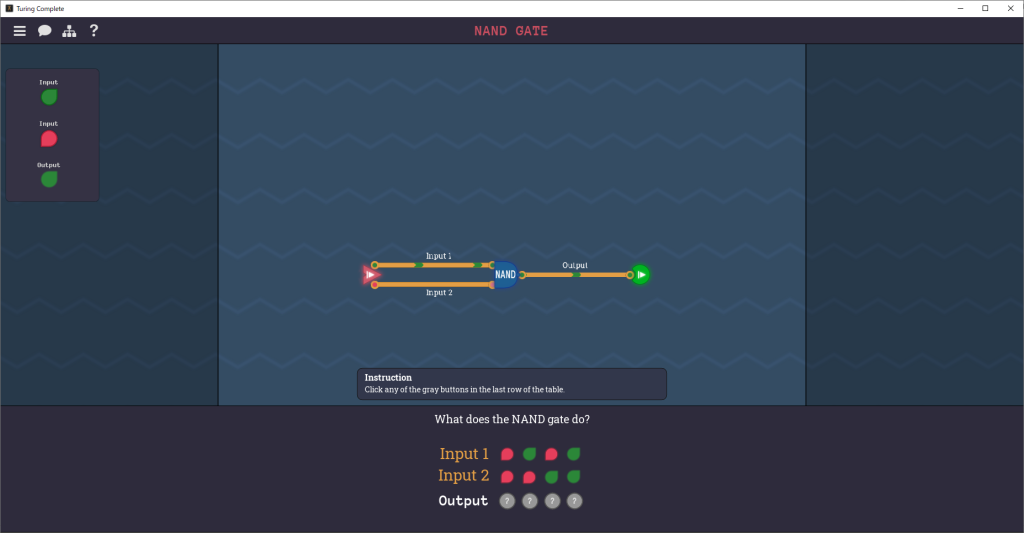
左側の2つのInputを操作して、下の真理値表（ON・OFFランプの表）を完成させます。

Outputが「？」となっているところを埋めていきます。

一般の真理値表が列と行が逆になっているので、ここでは1列ごとに見ていきます。

Input 1がOFF、Input 2がOFFのときに、Outputがどうなるのかという問題です。左上のInputを操作して、画面中央の回路において出力の「＞」の色を確認します。緑色（ON）になっているので、Outputの？をクリックしてONを選びます。

これを最後の4列目まで実施します。

すべての？を埋めると、[Check]ボタンが表示されます。[Check]ボタンを押し、Outputがすべて正解なら"Correct!"というメッセージが表示されます。

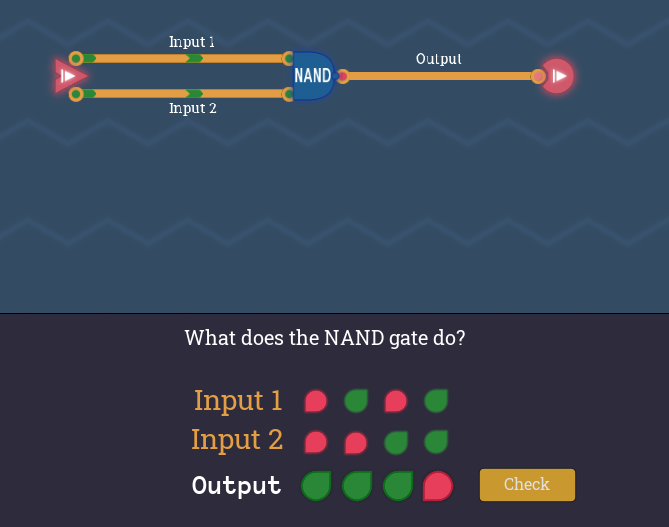
メッセージから、以降はNANDゲートからすべてを作り上げることが読み取れます。

NANDゲートがアンロックされ、以降使えるようになります。

NANDゲートの真理値表に慣れるまでの考え方

NANDゲートの真理値表がぱっと思いつかない場合は、「NAND＝AND＋NOT」のように段階を追って考えるとよいでしょう。

※NANDという名称は「AND」の「NOT」と考えるとよいでしょう。同様にしてNORは「OR」の「NOT」と推測できるようになります（覚える必要がなくなる）。

※私はよくそうしています。

まずANDの真理値表を想像します。AND演算は入力が全部Tのときだけ出力がTになります。

※慣れるまでは紙に書いてもよいでしょう。

次に、その出力に対するNOTを考えます。

a	b	AND(a,b)	NOT(AND(a,b))
0	0	0	1
0	1	0	1
1	0	0	1
1	1	1	0

NOT(AND(a,b))の真理値表は、上に示したNAND(a,b)の真理値表と一致しています。

コンピュータアーキテクチャーを設計する際にはNANDゲートからスタートしますが、真理値表だけを考えるのであれば、NANDゲートはANDゲートとNOTゲートの組み合わせと考えた方がわかりやすいです。

NOT Gateステージ

NOT Gateステージのゴールは、入力が1つしかなく、出力には常に入力の論理値が判定したものが現れる回路を組むことです。

このような入出力を持つ回路をNOT回路（論理否定回路）といいます。

NANDコンポーネントをを手に入れたので、これを使ってNOT回路を構成することになります。

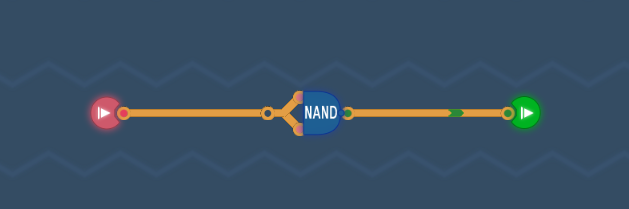
真理値表

a	NOT(a)
0	1
1	0

トランジスターで作成するNOT回路

NOT回路は1個のトランジスターで構成できます。

AND Gateステージ

AND Gateステージのゴールは、2つ以上の入力があり、すべての入力が1のときにだけ出力が1になる回路を組むことです。

このような回路をAND回路（論理積回路）といいます。

考え方は簡単です。

NANDゲートは「AND＋NOT」だったわけなので、出力をもう一度NOTゲートを通せば、ANDだけと同等のになります。

NOT(NOT(a))=aだからです。

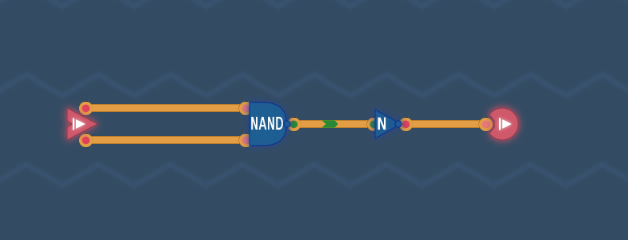
真理値表

a	b	AND(a, b)
0	0	0
0	1	0
1	0	0
1	1	1

ダイオードで作成するAND回路

ダイオードが2本あればAND回路を作成できます。

NOR Gateステージ

NOR Gateステージのゴールは、2つのビットを入力とし、一方でもONなら、OFFを出力する回路を組むことです。

NANDの出力にNOTを追加するとANDになりました。では、加えて2つの入力にNOTを追加したらどうなるでしょうか。

それがNORゲートです。

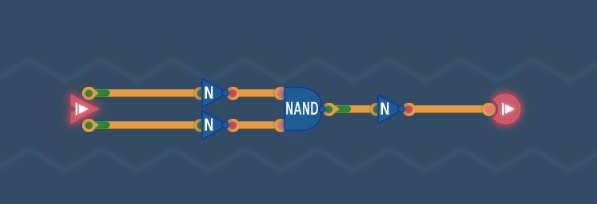
真理値表

NORは「OR＋NOT」と考えられます。

a	b	OR(a, b)	NOR(a, b)
0	0	0	1
0	1	1	0
1	0	1	0
1	1	1	0

OR Gateステージ

OR Gateステージのゴールは、2つの入力があり、いずれか1つでもONであれば出力がONになる回路を組むことです。

2つ以上の入力があり、いずれか1つでも1であれば出力が1になる回路のことをOR回路（論理和回路）といいます。

NORゲートは「OR＋NOT」と考えれば、出力にNOTを追加すれば、ORゲートになると気づきます。

NOTゲートが2連続になっているところはON・OFF的には取り除いて問題ありません。

見た目がすっきりしますし、ゲートの無駄遣いが少なくなります。

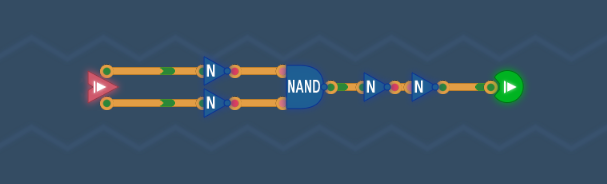
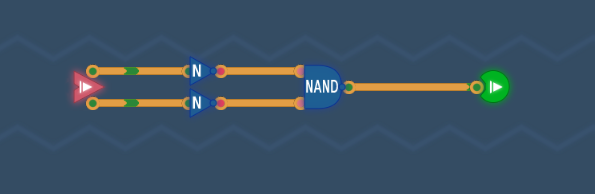
真理値表

a	b	OR(a, b)
0	0	0
0	1	1
1	0	1
1	1	1

ダイオードと抵抗器で作るOR回路

2本のダイオードと1本の抵抗器があればOR回路を作れます。

Always Onステージ

Always Onステージのゴールは、常時ONを出力する回路を組むことです。

OR回路は片方が1であれば、出力は常に1になります。

よって、同一ルートから分岐させて片方にNOT回路を通せば、2入力のどちらかは常に1になります。

具体的な回路は次の通りです。

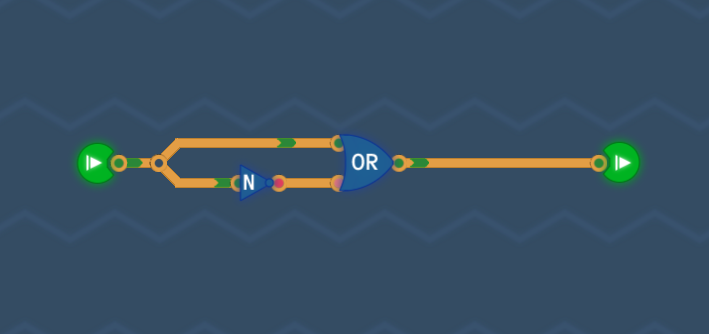
クリアすると、常時ONと常時OFFのコンポーネントを扱えるようになります。

インプット端子につながないバージョン【別解】

Second Tickステージ

Second Tickステージのゴールは、指定の真理値表を満たす回路を組むことです。

※メッセージはゲームの設定上の話であり、ヒントはありません。

慣れていないと即答はできないかもしれません。

ここではデジタル回路の超初心者を対象にしていますので、もっとも素朴なアプローチを紹介します。

使えるコンポーネントは以下の通りでありまだ少ないので、総当たりで調べてしまうのです。

※右の2つ（ONとOFF）は使わないので、コンポーネントの候補は5つになります。

今回の回路は2入力なので、内部に必ず2入力コンポーネントを使うはずです。NOR、NAND、OR、ANDのどれかを1つ画面の中央に置きます。

「置いたコンポーネントの入出力」と「回路の入出力」を単につないだだけでは、そのゲートを意味するだけになります。

目的の真理値表は、アンロックしたコンポーネントの真理値表と若干異なるので、どこかが違うわけです。

まずはシンプルに線1本のどこかにNOTを挟んでみます。これをひらすらやって、[RUN]ボタンを押して総当たりします。

※真理値表を見ると、Input 1とInput 2に対して対称的でないため、Outputにつながる線をいじるより、Inputにつながる線をいじるのが正しいと推測できます。これで、総当たりの候補数をさらに絞られました。"Second Tick"という名称なので、Input 2に当たりをつけて、NOTを挟んでみてください。

ANDとNOTを次のようにつなぐと、目的の真理値表を満たすことが判明するはずです。

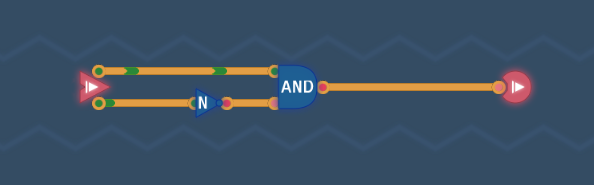
正解がわかってもすぐに次に進まずに、真理値表を紙に書いて、目的の真理値表と一致することを確認しておきましょう。

XOR Gateステージ

XOR Gateステージのゴールは、入力が一致のときにONを出力、不一致のときにOFFを出力する回路を組むことです。

このような動作をXORや排他的論理和と呼びます。EXOR（Exclusive Orエクスクルーシブ・オア）と書く場合もあります。どちらも同じです。

真理値表

2つの入力が異なる場合に1、それ以外は0を返します。

※対称的で美しく、覚えやすいといえます。「入力が異なるときだけTになる」というポイントだけ覚えればよいだけです。それ以外はFと自明に想像できます。

次はXORゲートの真理値表になります。a, bが入力、Yが出力です。

a	b	Y (=XOR(a,b))
0	0	0
0	1	1
1	0	1
1	1	0

論理式

真理値表から論理式を求めると、次のようになります。

$Y=\bar{A} \cdot B + A \cdot \bar{B}$

意味を考えるとXOR回路は不一致回路

不一致回路とは、入力信号が互いに異なるときに出力がHレベルになる回路です。

2入力の場合は、一方がHレベルで他方がLレベルのときに、出力がHレベルになる回路になります。

これはXORゲートの定義と一致しています。

つまり、XOR回路は（2入力の）不一致回路というわけです。

XORに関する公式

XORは特徴的な性質を持っているので、公式を知っておくと便利です。無理に覚えなくても、自力で真理値表から導けるようにしておきｍさよう。

[1]bが0固定のとき

⇒真理値表の1行目と3行目に注目する

a	b	XOR(a,b)
0	0	0
0	1	1
1	0	1
1	1	0

よって、bが0固定のとき、aがそのまま出力されています。公式化すると、次のようになります。

$a \, \text{XOR} \, 0=a$

[2]b=1固定のとき

⇒真理値表の2行目と4行目に注目する。

a	b	XOR(a,b)
0	0	0
0	1	1
1	0	1
1	1	0

よって、bが1固定のとき、aがビット反転されて出力されています。公式化すると、次のようになります。

$a \, \text{XOR} \, 1=\bar{a}$

[3]a=bのとき

⇒真理値表の1行目と4行目に注目する。

a	b	XOR(a,b)
0	0	0
0	1	1
1	0	1
1	1	0

よって、a=bのとき、常に0を出力します。公式化すると、次のようになります。

$a \, \text{XOR} \, a=0$

※この事実はアセンブリー言語において、レジスターをゼロクリアーするときに用いられるテクニックです。

XOR Gateステージを解く

真理値表はシンプルですが、構成しようとすると結構複雑になります。

真理値表がきれいな対称なので、内部構造も対象になると想像できます。

一致回路から不一致回路に拡張する【解答】

XOR回路は（2入力の）不一致回路と説明しました。

不一致回路は、一致回路の出力にインバーターを通せば完成するはずです。

意味的には正しそうですが、これを論理式で確かめておきます。Xを一致回路の出力、Yを不一致回路の出力、Zを一致回路の出力を反転させた結果とします。

$Z=\bar{X}$

$= \overline{ \bar{A} \cdot \bar{B} + A \cdot B }$

$= (\overline{\bar{A} \cdot \bar{B}}) \cdot (\overline{ A \cdot B}) $　（∵ド・モルガン則）

$= (\bar{\bar{A}} + \bar{\bar{B}}) \cdot (\bar{A}+ \bar{B}) $　（∵ド・モルガン則）

$= (A + B) \cdot (\bar{A}+ \bar{B}) $　（∵対合則）

$= (A + B) \cdot \bar{A} + (A + B) \cdot \bar{B} $　（∵分配則）

$= A \cdot \bar{A} + \bar{A} \cdot B + A \cdot \bar{B} + B\cdot \bar{B} $　（∵交換則、分配則）

$= \bar{A} \cdot B + A \cdot \bar{B} $　（∵補元則、変換則）

$=Y$

確かに一致回路の出力を反転させると、不一致回路になりました。

そこで、先に一致回路を組んでから、インバーターを通すというアプローチで考えてみます。

どうしてこうした回りくどいアプローチを採用するのかというと、不一致回路をいきなり設計するより、一致回路であれば設計しやすいからです。

1：一致回路を設計する

一致回路の真理値表は次の通りです。

A	B	X
0	0	1
0	1	0
1	0	0
1	1	1

次に真理値表から論理式を求めます。

$X=\bar{A} \cdot \bar{B} + A \cdot B$

この論理式を回路を組みます。

今回はうまい具合に積（$\bar{A} \cdot \bar{B}$と$A \cdot B$）の和の形になっています。

積「・」はANDゲート、和「＋」はORゲート、バーはNOTゲートであることを考慮します。

$\bar{A} \cdot \bar{B}$はNOTゲートに通した2入力をANDゲートに通せば実現できます。

$A \cdot B$はANDゲートそのものです。

最後に、上記の2つの結果をORゲートの入力とすれば完成です。

完成した回路は次の通りです。

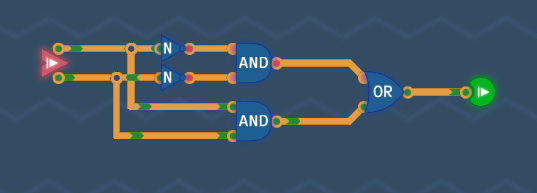
[Run]ボタンを押しても当然失敗するので、[Next]ボタンを押していき、XOR回路とまったく反対の結果になることを確認します。

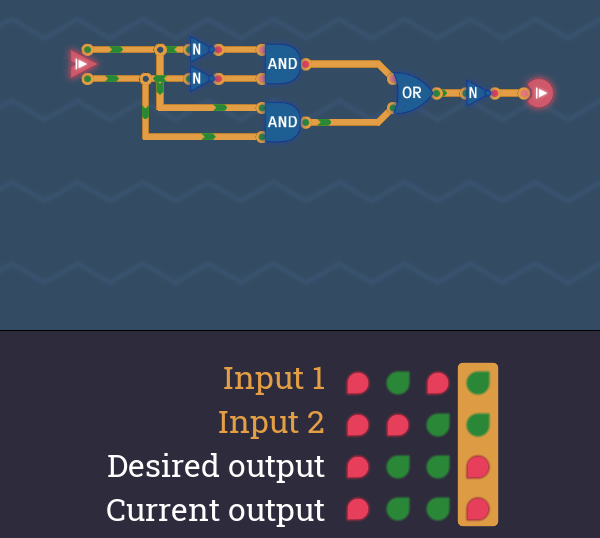
2：一致回路の後にインバーターを通して不一致回路にする

ステップ1で作った一致回路の出力の後にNOTゲートを配置します。

これで完成です。

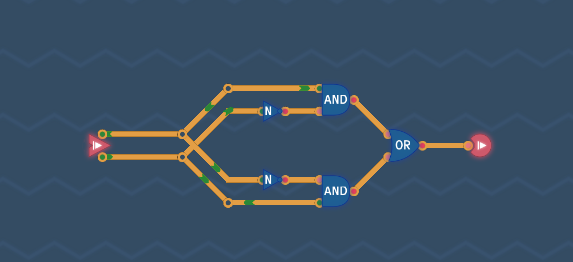
論理式から回路を組む【別解】

XOR回路の論理式は$Y=\bar{A} \cdot B + A \cdot \bar{B}$でした。

これから自然に回路を組むと次のようになります。

ただし、見やすいように対称的に配置しました。

XORゲートで構成する【別解2】

XOR回路の論理式を次のように変形していきます。

$Y=\bar{A} \cdot B + A \cdot \bar{B}$

$= (\bar{A} \cdot B + A) \cdot (\bar{A} \cdot B + \bar{B})$

$= (A + \bar{A}) \cdot (A+B) \cdot (\bar{A} + \bar{B}) \cdot (B + \bar{B})$

$= (\bar{A} + \bar{B}) \cdot (A + B)$

$= (\bar{A} + \bar{B}) \cdot A + (\bar{A} + \bar{B}) \cdot B$　←(*)

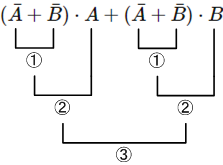
「和（①）→積（②）→和（③）」の形に変形できました。ここから回路を組みます。

この式を構成する論理回路は、「2段のNANDゲート⇒入力を反転してからORゲート」という回路になります。

4つのゲートの出力を次のように定義して、式を変形します。

$Y_1 \buildrel \rm def \over {:=} NAND(A,B) = \bar{A} + \bar{B} =\overline{A \cdot B}$

$Y_2 \buildrel \rm def \over {:=} NAND(A,Y_1) = \bar{Y_1 + A} = \overline{( \bar{A} + \bar{B} ) \cdot A} $

$Y_3 \buildrel \rm def \over {:=} NAND(Y_1,B) = \bar{Y_1 + B} = \overline{( \bar{A} + \bar{B} ) \cdot B} $

$Y \buildrel \rm def \over {:=} OR(NOT(Y_2), NOT(Y_3)) = \overline{Y_2 \cdot Y_3} = \overline{ \overline{( \bar{A} + \bar{B} ) \cdot A} \cdot \overline{( \bar{A} + \bar{B} ) \cdot B} } = (\bar{A} + \bar{B}) \cdot A + (\bar{A} + \bar{B}) \cdot B $

「Y=(*)」を証明できました。

Turing Completeのシミュレーターで回路を組んでテストして問題ないことを確認します。

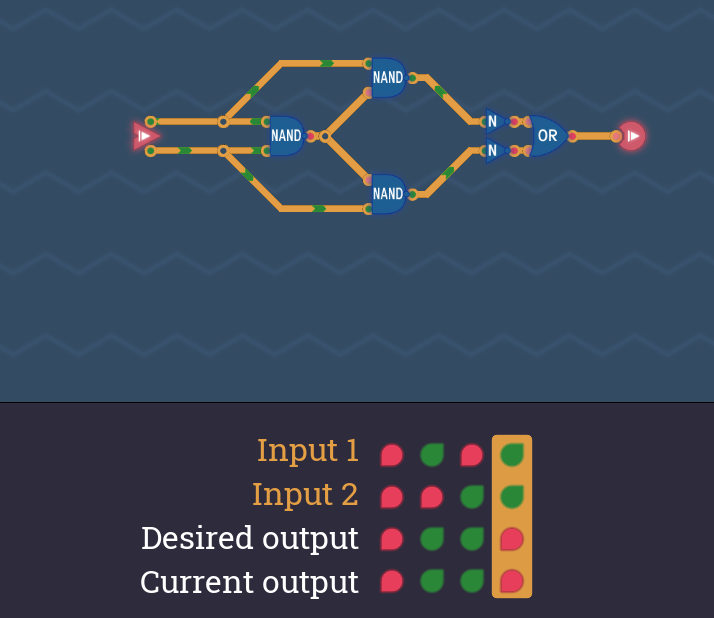
NANDだけで構成する【別解3】

次のように4つのNANDを配置するとXORゲートを構成できます。

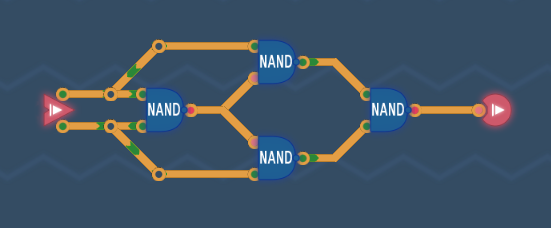
NAND、OR、ANDで構成する【別解4】

内部構造が一見して対称的に見えませんが、次のような回路でもXORゲートを構成できます。

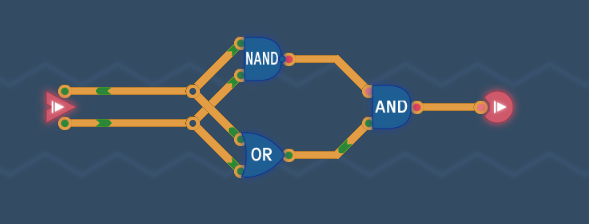
別解2はNAND、OR、ANDという3つの素子で作られていますが、それぞれ内部的にはNANDが1個、3個、2個になります（NOTはNANDゲート1個で作られる）。つまり、合計NAND6個使っていることになります。

アプローチ1はNANDが4個だけでした。

よって、NANDが少ない別解1の方が効率がよいといえます。

※それだけ遅延が少なくなります。

XOR回路からNOT回路やバッファ回路を作る

XOR回路の入力の片方をLにつなげるとバッファ回路、HにつなげるとNOT回路と同等になります。

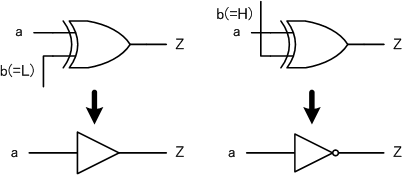
これが正しいかは、真理値表を書いてみればわかります。

※「L（low）=0=F（false）」「H（high）=1=T（true）」としています。

a	b（L固定）	Z(=XOR(a,b))
0	0	0
1	0	1

a	b（H固定）	Z(=XOR(a,b))
0	1	1
1	1	0

左側の回路の真理値表はバッファ回路、右側の回路はNOT回路と同等であることがわかりました。

XOR回路の特徴と応用

• XOR回路は「入力が一致しているときにLを出力し、入力が一致していないときにHを出力する」という回路だった。
  • XOR回路は2つのデータの一致や不一致を調べられるということ。
• データの大小の判断を行う比較器の基本回路になる。
• いろいろな演算をする演算器の基本回路になる。

Bigger OR Gateステージ

ここから多入力の基本ゲートを作ります。

Bigger OR Gateステージのゴールは、多入力OR回路を組むことです。

nビットの入力のうち、少なくとも1つがHなら、Hを出力します。それ以外の場合はLを出力します。

入力が増えても考え方はシンプルです。ORゲートを多段すればよいだけです。

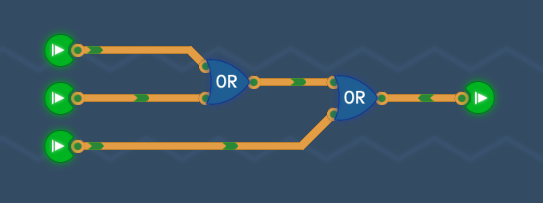
クリアすると3入力型ORコンポーネントがアンロックします。

Bigger AND Gateステージ

Bigger AND Gateステージのゴールは、多入力AND回路を組むことです。

これも考え方は変わりません。

nビットの入力のうち全部がHであれば、Hを出力します。そうでなければLを出力します。

シンプルにANDゲートを多段すればよいだけです。

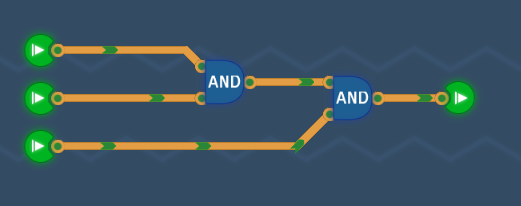
クリアすると3入力型ANDコンポーネントがアンロックします。

XNOR Gateステージ

XNOR Gateステージのゴールは、XORのNOT版の回路を組むことです。

XORの出力にNOTをつなげればよいことがわかります。

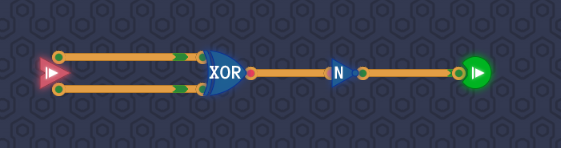
クリアするとXNORコンポーネントがアンロックします。

基本ゲートをもっと楽しみたい

オープンソースのICセルを3Dプリント