Binary RacerとDouble Trouble【Turing Complete編】

2023年8月15日2024年9月23日

1 はじめに
2 Binary Racerステージ
3 秘密の実績「Binary Racer」を解く
- 3.1 人力で解く
- 3.2 支援プログラムを使う
4 Double Troubleステージ
5 Double Troubleステージの解決アプローチ
- 5.1 「3入力のうち、2つ以上Tなら、Tを出力する」回路を考える
6 Double Troubleを解く
- 6.1 XOR回路とAND回路を組み合わせる【別解】
7 おわりに

はじめに

いつもブログをご覧いただきありがとうございます。

コーストFIRE中のIPUSIRONです😀

IPUSIRONのプロフィールを見る

Binary Racerステージ

10進数で値が表示されるので、2進数に対応するスイッチをON・OFFします。

時間制限で次々に問題が出題されます。

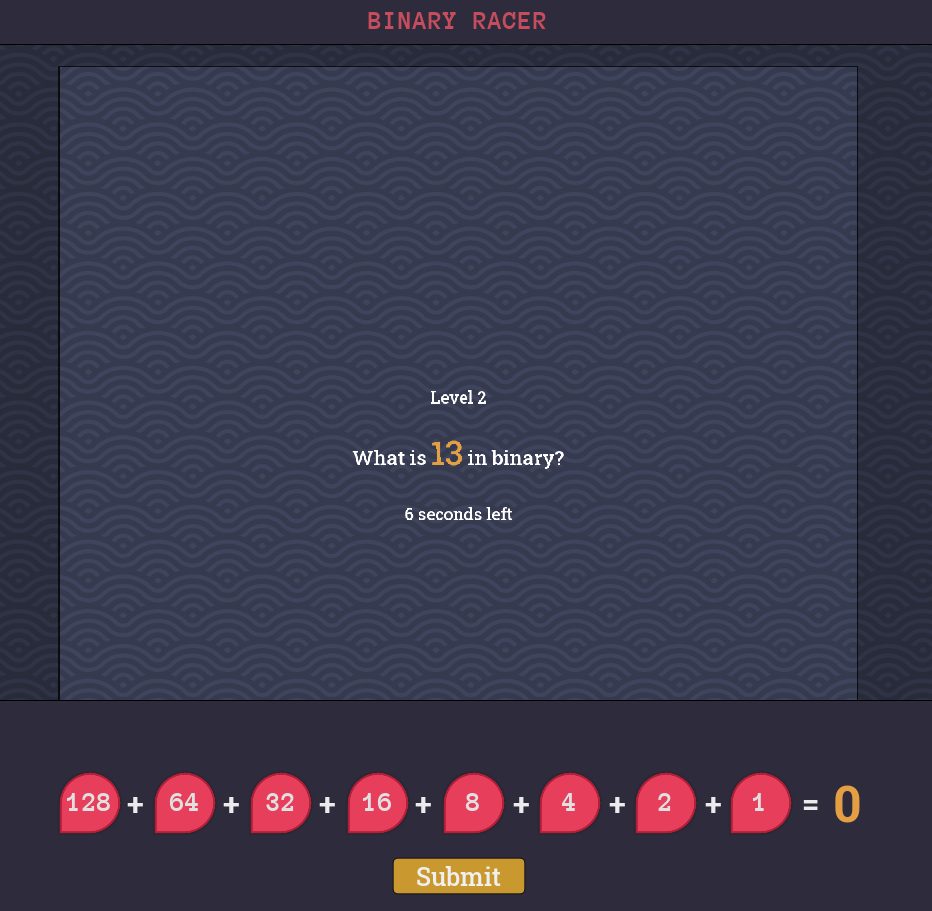
脳内で2進数に変換してからON・OFFするのもよいですが、即答できなければ下のスイッチの数を参考にしてON・OFFして検算してから[Submit]ボタンを押せばよいでしょう。

慣れれば、例えば63が出題されたら、64のスイッチより右側を全部ONにすればよいこともわかります。

秘密の実績「Binary Racer」を解く

実績「Binary Racer」のゴールは、最高のレベル7をクリアすることです。

人力で解く

レベル6になると全ビットを使うパターンが出てきます。つまり、128以上の数が出てきます。計算ができたとしても、各ビットをトグルするだけでも時間を食います。

小さい数の簡単な問題が出てきたら、すぐに[Submit]ボタンを押さずに落ち着く時間を確保するようにしましょう。

勘と運を頼りにミジンコレベルでもレベル6にまではなんとかいけました。

噂ではレベル7ではトグルしたビットの合計数が表示されないようです。10進数から2進数への変換を暗算かつ即答できなければきついでしょう。

ビット列の各桁は[1]～[8]キー、[Submit]キーは[Space]キーに対応しています。マウス操作を止めて、キーボード操作だけで問題を解けば、スピードアップを見込めるかもしれません。

2人で解くという方法も有効かもしれません。1人目はトグル担当、2人目は何らかのソフトウェアを使っての2進数への変換担当とするのです。作業の内容によって担当を分けることで高速化が期待できます。

支援プログラムを使う

何時間も練習し続けるより、支援プログラムを作った方がよいかもしれません。

例えば、出題の10進数を入力したら、自動でトグルするようなプログラムです。マウスのクリック位置を調整するようにプログラム内の座標を書き換える必要があるでしょう。

Steam Community :: Guide :: Achievements

Solution to all achievements...

https://steamcommunity.com/sharedfiles/filedetails/?id=27984...

Pythonの支援プログラムを作った

私はPythonで、次の2つのプログラムを作りました。

“GetXY.py"ファイル･･･画面上の座標を調べるプログラム。
“SolveBinaryRacer.py"ファイル･･･実績「Binary Racer」を解くためのプログラム。

各プログラムの中身は次の通りです。

import time
from pynput import keyboard, mouse

# マウスのイベントを処理する関数
def on_click(x, y, button, pressed):
    if pressed:
        print(f"Mouse clicked at ({x}, {y})")

# キーボードのイベントを処理する関数
def on_press(key):
    if key == keyboard.Key.space:
        print("スペースキーが押されました。プログラムを終了します。")
        return False  # キーボードリスナーを停止する

# リスナーを同時に起動する関数
def start_listeners():
    with mouse.Listener(on_click=on_click) as mouse_listener:
        with keyboard.Listener(on_press=on_press) as keyboard_listener:
            keyboard_listener.join()  # キーボードリスナーが停止するのを待つ
            mouse_listener.stop()  # キーボードリスナーが停止したらマウスリスナーも停止する

def main():
	time.sleep(5)	# 安全のために5秒待つ.

	print("クリックした座標の取得を開始します。")
	start_listeners()	# リスナーを起動

if __name__ == '__main__':
	main()

import pyautogui

# 座標は画面を調整・配置してから、GetXY.pyを利用して調べておく.
# 各桁に対応するボタンの座標.
coordinates = [
    (-1319, 864),  # 8ビット目
    (-1224, 867), # 7ビット目
    (-1130, 860), # 6ビット目
    (-1040, 861), # 5ビット目
    (-939, 861), # 4ビット目
    (-848, 861), # 3ビット目
    (-756, 869), # 2ビット目
    (-644, 867) # 1ビット目
]
# Submitボタンの座標.
point_submit = (-954, 934)

def click_coordinates(binary_value):
    # 8桁固定のバイナリ値を確認して、対応する座標をクリック
    for i, bit in enumerate(binary_value):
        if bit == '1':
            x, y = coordinates[i]
            pyautogui.click(x, y)

def main():
    try:
        while True:
            # ユーザーに10進数を入力させる
            decimal_number = int(input("Enter a decimal number (or press CTRL+C to exit): "))
            
            # 10進数を2進数に変換
            binary_number = bin(decimal_number)[2:].zfill(8)
            print(f"Binary representation: {binary_number}")
            
            # 元のマウスポインタの位置を取得
            original_position = pyautogui.position()

            # 各桁に対応するボタンを押す
            click_coordinates(binary_number)

            # Submitボタンを押す
            pyautogui.click(point_submit[0], point_submit[1])
            
            # マウスポインタを元の位置に戻す
            pyautogui.moveTo(original_position)
            pyautogui.click(original_position[0], original_position[1])
            
    except KeyboardInterrupt:
        print("\nProgram exited by user.")
        return

if __name__ == "__main__":
    main()

使い方としては、次の通りです。

1：Turing Completeの画面の大きさを調整、他のウィンドウと被らない位置に配置します。

Binary Racerステージを表示させておきます。適当なスイッチを押すと、[Submit]ボタンも表示された状態になっているはずです。

2：プログラムで呼び出されるライブラリーをインストールします。

PyAutoGUIライブラリを使うと、マウス操作やキーボード入力を自動化できます。

先にPIPを更新しておきます。コマンドプロンプトで次を実行します。

>python -m pip install --upgrade pip

pip installコマンドでPyAutoGUIをインストールします。

pip install pyautogui

エラーがでなければインストールされました。

3：PythonのIDLEを起動します。

PyAutoGUIライブラリの動作確認をしてみます。

import pyautogui
pyautogui.moveTo(300, 300, duration=5)

画面の左上端の座標が(0, 0)として、座標(300, 300)に5秒かけてマウスポインタが移動します。

4：メニューの「File」＞「Open」から"GetXY.py"ファイルを開きます。"GetXY.py"ファイルの画面が開いたら、メニューの「Run」＞「Run Module」を押します。

クリックしたところの座標が次々と表示されます。メインモニターの左上が座標の基準点になります。

※デュアルモニターで右側がメイン、左側がサブだとしします。サブモニター側のX座標はマイナスになるだけで、プログラムの実行に問題ありません。

Binary Racerステージの8つのスイッチの中央辺り、[Submit]ボタンの中央辺りをクリックして、座標を出力します。

終わったら[Space]キーを押して、プログラムを終了させます。

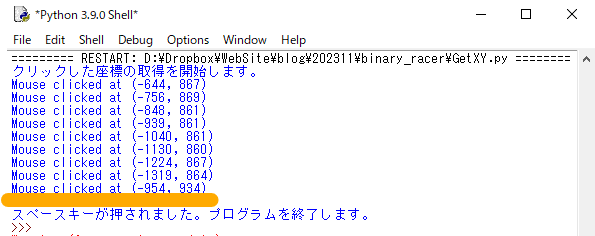
5："SolveBinaryRacer.py"ファイルには9つの座標が定数としてハードコーディングされています。

ここをステップ4で得られた座標に置き換えてください。各桁に対応する座標については、上位ビットから並んでいることに注意してください。

設定後に保存します。

メニューの「File」＞「Open」から"SolveBinaryRacer.py"ファイルを開きます。"SolveBinaryRacer.py"ファイルの画面が開いたら、メニューの「Run」＞「Run Module」を押します。

10進数の入力の待ち状態になったら準備OKです。

Binary Racerステージをスタートさせます。次々と中央に表示される10進数を、IDLE側で入力します。[Enter]キーで確定すると、マウスポインタが勝手に動いてBinary Racerステージ側のスイッチを自動で押してくれます。そして、IDLE側のカーソルが戻り、続けて次の10進数を入力できます。

我々がやるべきことは、目視で見た10進数を間違えないように入力するだけです。

6：レベル7が終わると、”Good job, you reached level 7.”というメッセージダイアログが表示されて、ステージクリアになります。

これで実績"Binary Racer"も解除されます。

今回のアプローチで改良の余地は残されています。
・座標調査プログラムとBinary Racerを解くプログラムを合体する。プログラム実行時に、指示通りにクリックするとプログラムに座標を保持し、そのデータを用いてBinary Racerを解くようにすればよい。
・10進数を目視で識別し、手動で入力するのではなく、これらを全自動にする。

Double Troubleステージ

4つの入力のうち、2つ以上の入力がONなら、出力をONにする回路を作ります。

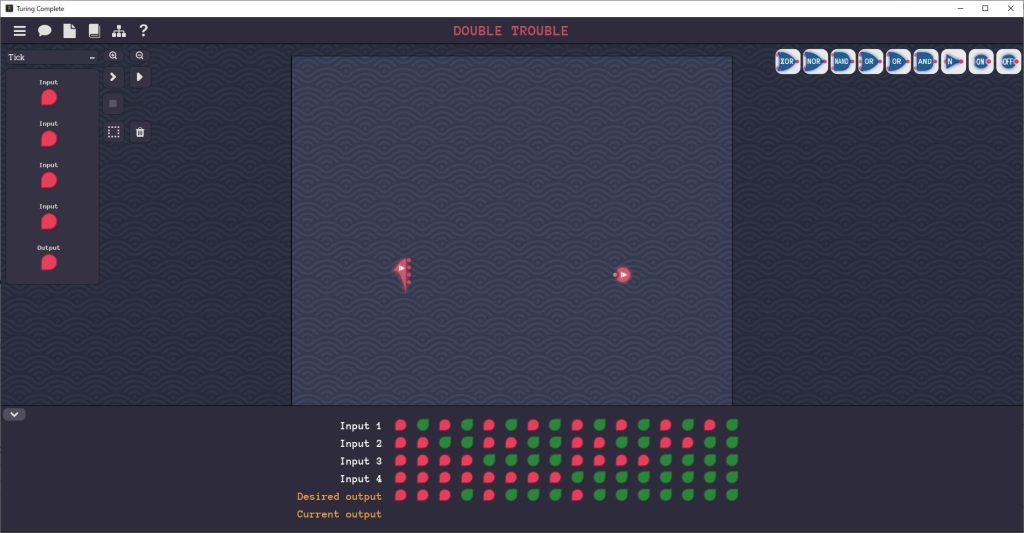
Double Troubleステージの解決アプローチ

最初に見るべきところは、4入力、1出力ということです。

※入力が4ビット、出力が1ビットとも言い換えられます。

「（4入力のうち）2つ以上がTのとき」は「2入力 or 3入力 or 4入力がTのとき」に分解できます。

※逆にいえば、「1入力がFのときのみ」と言い換えられます。

いきなり4入力では難しく感じてしまうので、数を小さくした例から考えていきます。

「2入力のうち1つでもTなら、Tを出力する」のがORゲートでした。

「3入力のうち1つでもTなら、Tを出力する」のが多入力ORゲートでした。

では「3入力のうち2つ以上がTなら、Tを出力する」回路はどうなるでしょうか。これがわかれば、「4入力のうち2つがTなら、Tを出力する」回路の参考になるかもしれません。

入力の全数	T出力時、Tを与えべき入力数	対応する回路
1	1	バッファーゲート or 単なるワイヤー or NOT(NOT)
2	1	ORゲート
2	2	ANDゲート
3	1以上（1,2,3）	多入力ORゲート（3入力型）
3	2以上（2,3）	？（今から考える回路）
3	3	多入力ANDゲート（3入力型）
4	1以上（1,2,3,4）	多入力ORゲート（4入力型）
4	2以上（2,3,4）	？（Double Troubleの回路）
4	3以上（3,4）	？
4	4	多入力ANDゲート（4入力型）

「3入力のうち、2つ以上Tなら、Tを出力する」回路を考える

ブログに載せるために画像はVisioで作成していますが、皆さんは紙に描いてください。

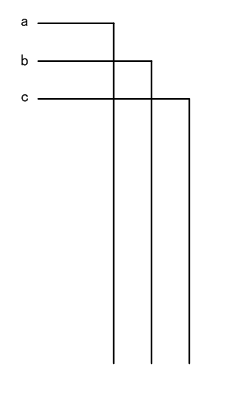
1：3入力から伸びるワイヤーを並べる

ワイヤーを折り返して、縦に伸ばします。

これで対称性を確認しやすくなると同時に、後段の位置するコンポーネントに接続しやすくなります。

※各コンポーネントの入力は左側にあるためです。もし、コンポーネントを90度回せれば、ワイヤーは横に伸びていた方が扱いやすいといえます。

2：回路を分割して考える

出力がTになるのは、2入力以上がTのときです。

言い換えれば「2入力がT or 3入力がT」のときです。

「2入力がTを判定する回路」（前段）と「それ以降の回路」（後段）に分けられそうです。

3：後段に当たりをつける

前段の判定でTと判定されたら、残りの1入力がTでもFでも、出力Tにしなければなりません。つまり、後段はORゲートが基本になると推測できます。

※まだこの時点ではORゲート単体なのか、多入力ORゲートなのかは不明とします。単にORゲートがメインとなることだけわかります。

4：前段を設計する

3本のワイヤーのうち、2つがTであるなら、前段の出力はTになります（それが後段の入力になる）。

2つがTなら出力がTになるゲートとして、ANDゲートがありました。これが活用できそうです。

ただし、3入力型ANDゲートを使えません。

代わりに、3本のワイヤーから2本を選択するにします。その組み合わせ数は3通りです。

※a,b,cのワイヤーがあり、2本を選ぶ組み合わせは(a,b)、(b,c）、(a,c）の3通りだからです。

これらの組み合わせをANDゲートの入力とします。

まずは図にAND(a,b)を追加します。

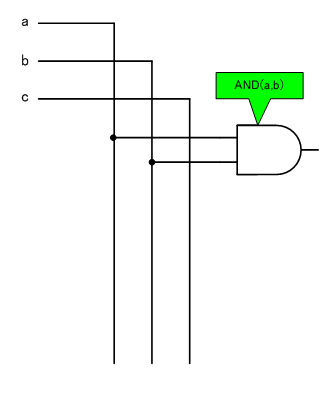
同様にして、AND(b,c)、AND(a,c)も追加します。

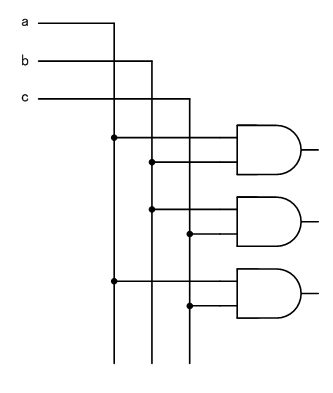
ここまでで上段が完成しました。

5：後段を設計する

後段の入力には3本のワイヤーがあります。

3入力のうち、1本でもTなら、出力をTにする回路を作り上げるのが目的です。

そのためには、多入力ORゲート（3入力型）を使うだけです。

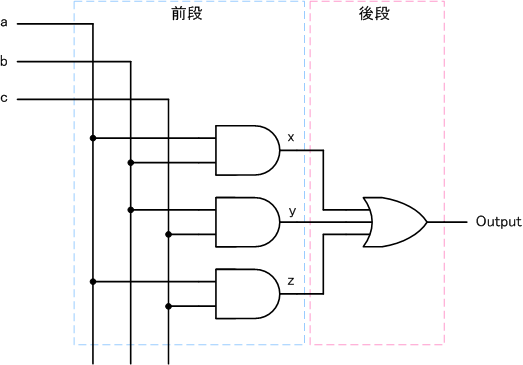
以上で回路が完成しました。

6：真理値表でチェックする

a	b	c	x	y	z	Output
F	F	F	F	F	F	F
F	F	T	F	F	F	F
F	T	F	F	F	F	F
F	T	T	F	T	F	T
T	F	F	F	F	F	F
T	F	T	F	F	T	T
T	T	F	T	F	F	T
T	T	T	T	T	T	T

Double Troubleを解く

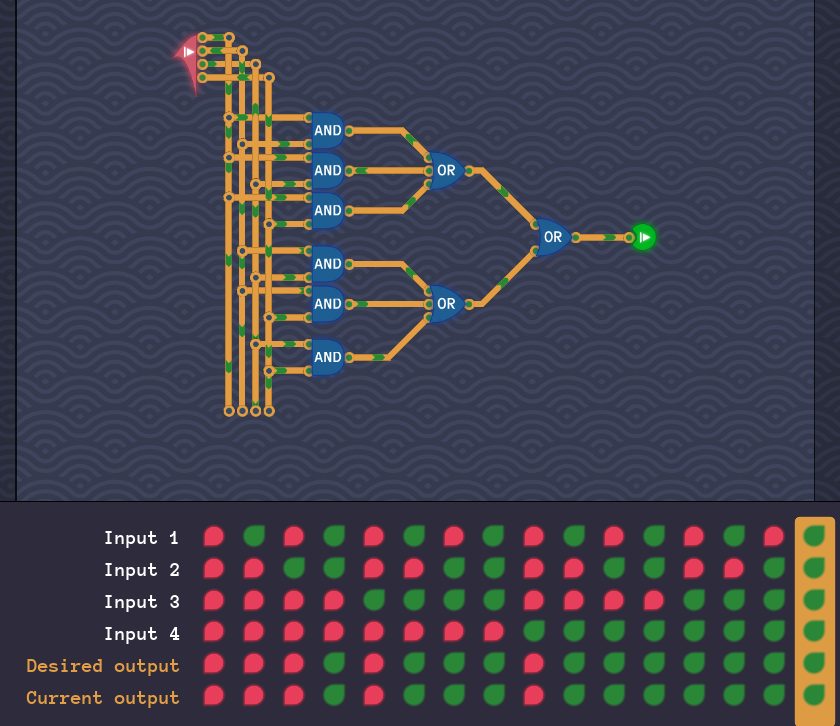
Double Troubleの回路は「4入力のうち、2つ以上Tなら、Tを出力する回路」です。

回路の設計は前述の流れにしたがって進めてみます。

1：4入力から伸びるワイヤーを並べる

前述の回路と見比べやすいように、Inputコンポーネントは左上に配置します。

ワイヤーを折り返して、縦に伸ばします。

2：段数を考察する

先ほどの回路では前段と後段に分けました。

今回は入力数が1本増えていますが、前段・後段の2つに分けて考えられます。

3：前段を設計する

先ほどと同様に考えて、4本のワイヤーから2本を選択してANDゲートの入力にします。

入力をa,b,c,dとすれば、その組み合わせは6通りです。高校で習うコンビネーションで簡単に計算できます。

₄C₂=(4・3)/(2・1)=6

具体的にいえば、(a,b)、(a,c)、(a,d)、(b,c)、(b,d)、(c,d)の組み合わせになります。

6個のANDゲートを縦に並べて、具体的な組み合わせを参考にしてANDゲートの入力に接続していけばよいのです。

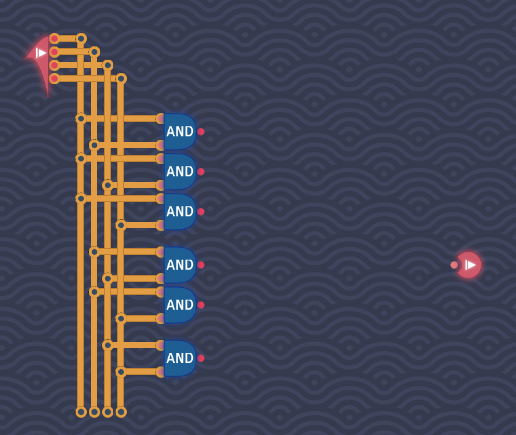
4：後段を設計する

前段からは6つの出力があるので、後段の入力は6入力です。

後は、これらをORで結べばよいだけです。

6入力型多段ORゲートがあればよいのですが、手元には（2入力型）ORゲートと3入力型多段ORゲートしかありません。

使えるOR系のコンポーネントを使って、6入力型多段ORゲートを構成することにします。

やり方はいろいろありますが、先に3入力型多段ORゲートで束ねてしまいましょう。後は、ORゲートに通すだけです。

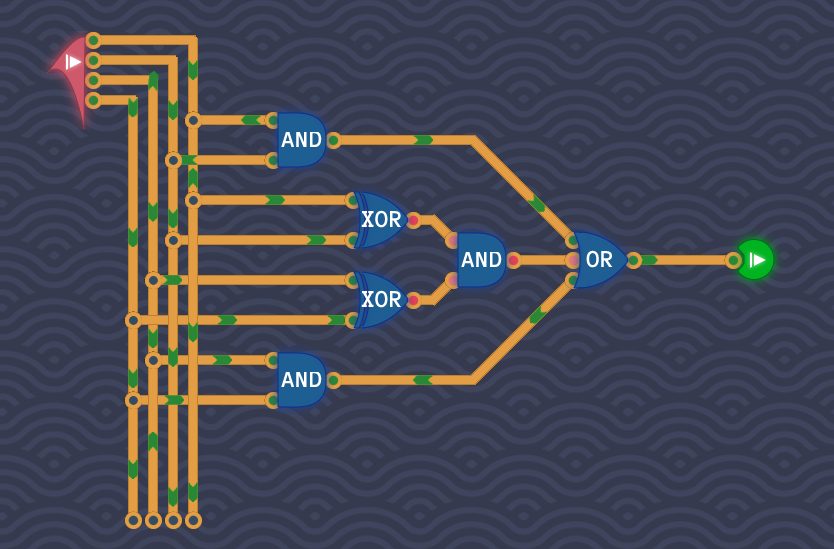
XOR回路とAND回路を組み合わせる【別解】

おわりに

最初は自力でなかなか回路を導けないことが多いかもしれません。
また回答を読んでもピンとこないこともあるでしょう。
そうであっても諦めたり、立ち止まったりする必要はありません。
こうした回路を構成するのは、一種のクイズを解くようなものです。クイズが解けないからといって、高度な仕組みの理解とはまた別問題といえます。
Turing Completeでは、コンポーネントの中身がわからなくても、以降は入出力だけに注目して使うことになります。
つまり、中身はブラックボックスとしても問題ないわけであり、以降の学習にあまり影響しないので安心してください。
デジタル回路の世界になれれば、自然と自力で回路を組めるようになるはずです。

Turing Complete2進数,デジタル回路

Posted by ipusiron

Odd Number of Signals【Turing Complete編】

Basic Logic【Turing Complete編】