Half AdderとFull Adder【Turing Complete編】
目次
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
加算器は全加算器で
加算器は次の3つに大別されます。
| 半加算器 | 2つのビットの和を求める回路。 ・入力:A, B・・・計2ビット ・出力:S, CO(キャリーアウト)・・・計2ビット S=A+Bの最下位ビット CO=A+Bの最上位ビット |
| 全加算器 | 3つのビットの和を求める回路。 ・入力:A, B, CI(キャリーイン)・・・計3ビット CI・・・前段からの桁上げ用 ・出力:S, CO・・・計2ビット S=A+B+CIの最下位ビット CO=A+B+CIの最上位ビット |
| 多ビット加算器 (単に加算器といったらこれ) | 2つのnビットの和を求める回路。 ・入力:A[n], B[n]・・・計2nビット ・出力:Out[n]・・・nビット ※2の補数による加算。 ※オーバーフローは検出しない。 |
2進数の加算を考える
2進数の加算を表にすると次のようになります。
| + | 0b | 1b |
| 0b | 00b | 01b |
| 1b | 01b | 11b |
加算した結果は(最大)2ビットになります。
この2ビットはサムアウトとキャリーアウトから成るものと考えます。それぞれは1ビットを強調して、次のように呼ぶこともあります。
- サムアウト=サムビット=和ビット
- キャリーアウト=キャリービット=繰り上げビット=桁上げビット
半加算器
半加算器(ハーフアダー)は、下の桁からの桁上がりを考慮しない加算を実現する回路です。
ブロック図
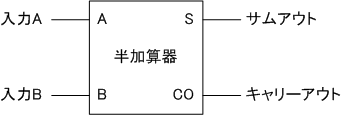
真理値表
| A | B | S | CO |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
論理式
真理値表から論理式が論理式が得られます。
$S= \bar{A} \cdot B + A \cdot \bar{B}$
$CO = A \cdot B$
Half Adderステージ
半加算器を作る問題です。
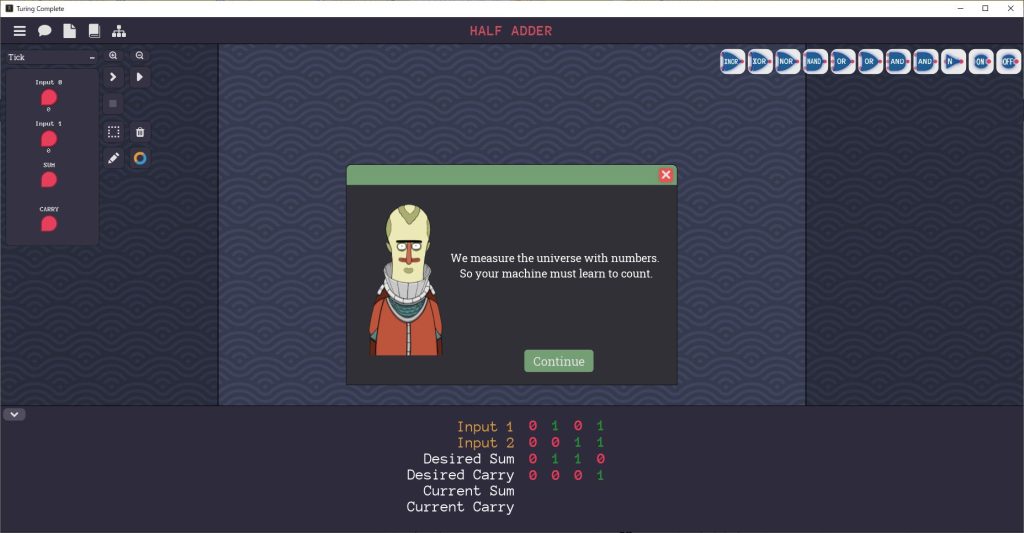
Half Adderステージを解く
それでは問題を解いていきましょう。
1:サムアウトとキャリーアウトだけに注目した加算表を作る
1ビットの加算表のままだと内部回路を考えにくいので、サムアウトとキャリーアウトそれぞれに注目した加算表を書き出します。
| + サムアウト | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| + キャリーアウト | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
2:サムアウトの加算表はXOR回路そのもの
サムアウトの加算表をよく見ると、XOR回路の真理値表と同一です。
XORコンポーネントを配置します。
そして、2入力をXORコンポーネントの入力につなげて、XORコンポーネントの出力をSUMにつなげます。
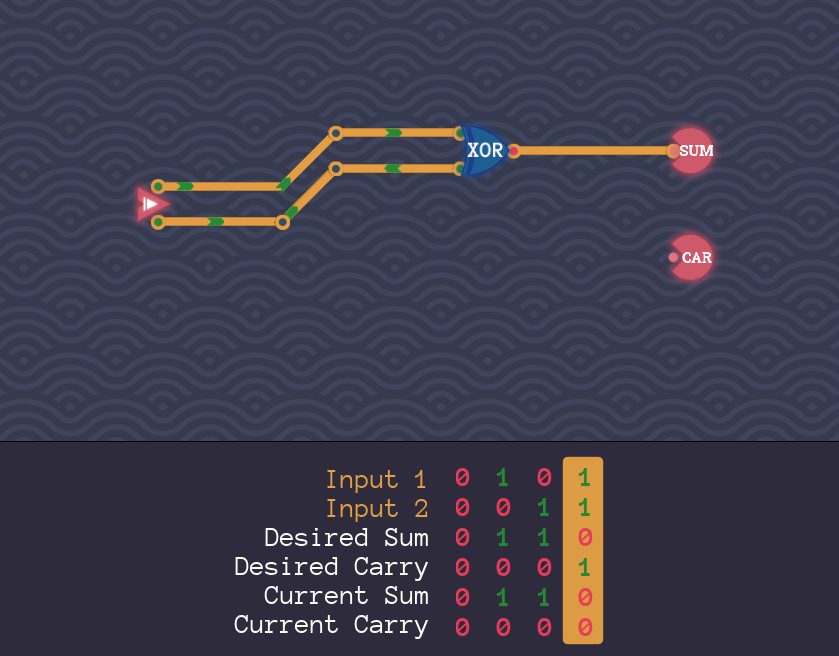
全パターンをテストして、Desired Sum(Half Adderの満たすべきサムビット値)とCurrent Sumが一致することを確認します。
※[Run]ボタンを押すと、最後のパターンだけエラーになりますが、これはキャリーアウト値で不一致が発生しているからです。キャリーアウトについてはまだ未配線なので失敗するのは当たり前です。
3:キャリーアウトの加算表はAND回路そのもの
キャリーアウトの加算表をよく見ると、AND回路の真理値表と同一です。
ANDコンポーネントを配置します。
そして、2入力をANDコンポーネントの入力につなげて、ANDコンポーネントの出力をCARにつなげます。
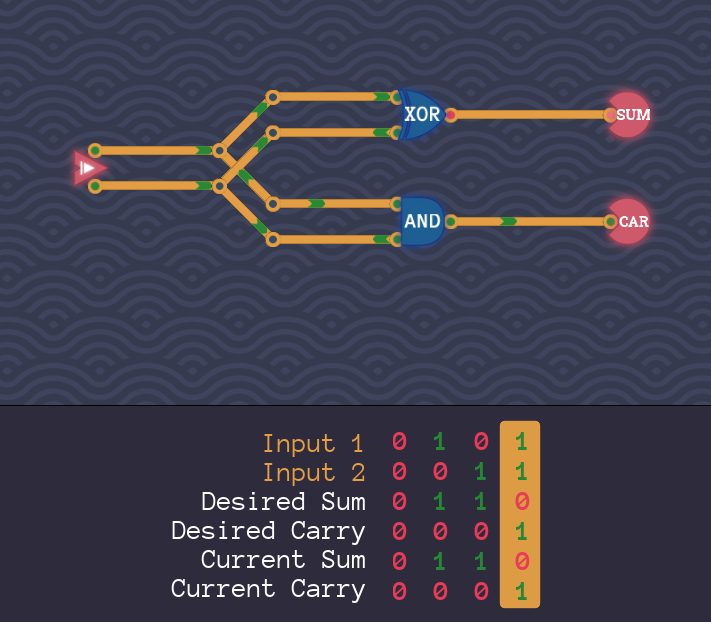
4:テストします。
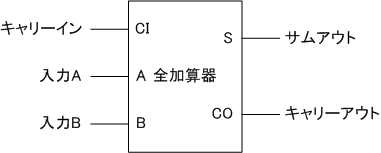
全加算器
全加算器(フルアダー)とは、下の桁からの桁上がりを考慮に入れた加算を実現する回路です。
ブロック図
真理値表
入力:A、B、C
出力:S、CO
| A | B | CI | S | CO |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
キャリーインで場合分けする
キャリーインが0か1かで場合分けしたうえで、加算表を作るのです。
(a)キャリーインが0のとき
| + サムアウト | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| + キャリーアウト | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
※キャリーインが0の場合は、キャリーインが存在しない半加算器と同等になります。
(b)キャリーインが1のとき
| + サムアウト | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| + キャリーアウト | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
※半加算器の加算表において、すべての欄で+1した結果になります。
Full Adderステージ
全加算器を作る問題です。
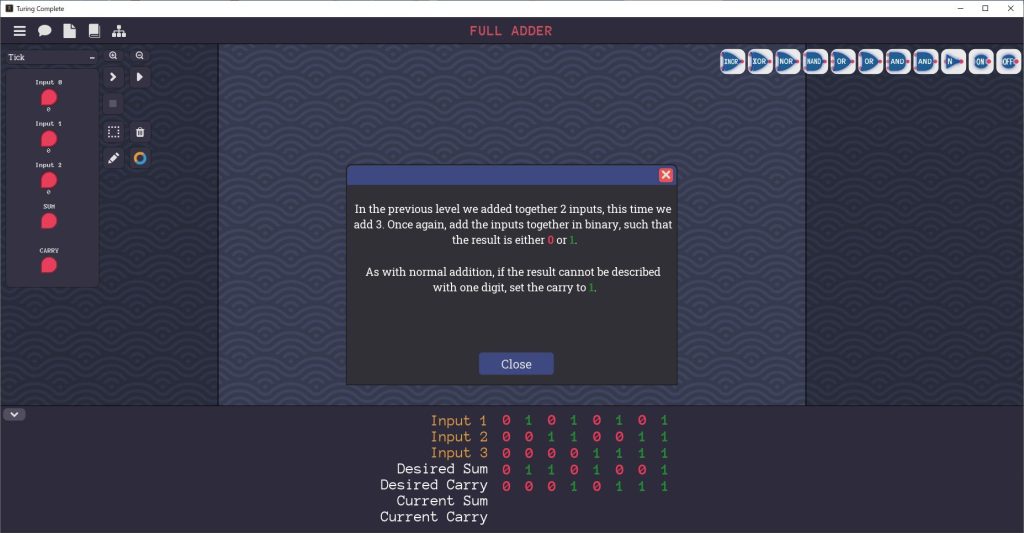

Full Adderステージを解く
半加算器のブロック図を使って、全加算器を構成すると次のようになります。
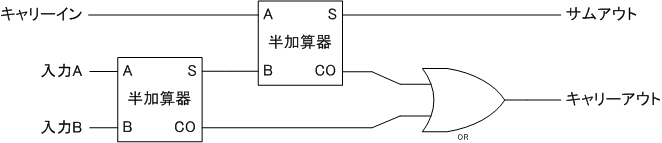
現時点のTuring Completeで半加算器コンポーネントが使えれば簡単なのですが、残念ながら使えません。
※前の問題で半加算器を解いても、半加算器はアンロックされません。
半加算器の中身の回路をそのまま基本ゲートで実現したバージョンは次の通りです。
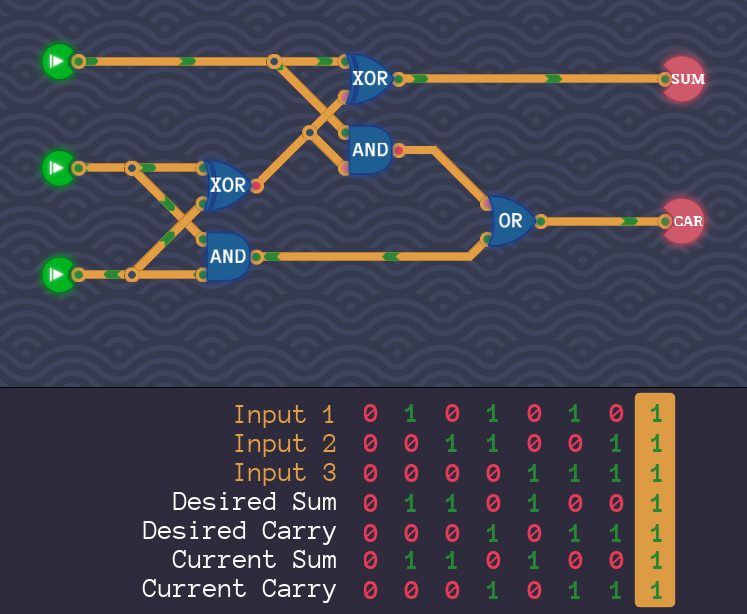
Turing CompleteのInput 1~3がA, B, CIのどれに対応するかは本質的ではありません。なぜならどれも1ビットであり、加算時は同等に扱えるためです。
ここでは、ブロック図に比較して見やすくするために、Turing CompleteのInput 1はCI、Input 2はA、Input 3はBに対応させました。
クリアすると、Full Adderコンポーネントがアンロックされます。