Byte OR、Byte Not、Adding Byte【Turing Complete編】
目次
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
Byte ORステージ
Byte ORステージのゴールは、2つの8ビット値をOR演算する回路を組むことです。
【入力】
・Input 1・・・8ビット
※2進数の8ビットは、10進数で(符号なしなら)0~255を表現できます。
・Input 2・・・8ビット
【出力】
・Output・・・8ビット
左を見るとInputやOutputに8個のランプが並んでいます。
1ビットのワイヤーが8本束になっているということです。
これは8ビットのワイヤーと同等です。
シミュレーター上では8ビットのワイヤー上に10進数値が流れて表示されます。
これは2進数値のままだとわかりにくいために10進数値で表記しているだけであり、実際には8ビットの2進数値が流れているわけです。


Byte ORステージを解く
1:8ビットワイヤーを1ビットごとに分離する
Byte Splitterコンポーネントを通して、各出力ピンから1ビットずつを取り出せます。

2:1桁目(1の位)を配線する
「Input 1の1桁目(1の位)」と「Input 2の1桁目(1の位)」をOR回路に通します。
その出力を8 Bit Makerコンポーネントの1桁目(1の位)の入力につなげます。
これで8ビット全体のうち1桁目のOR演算が完了したことになります。
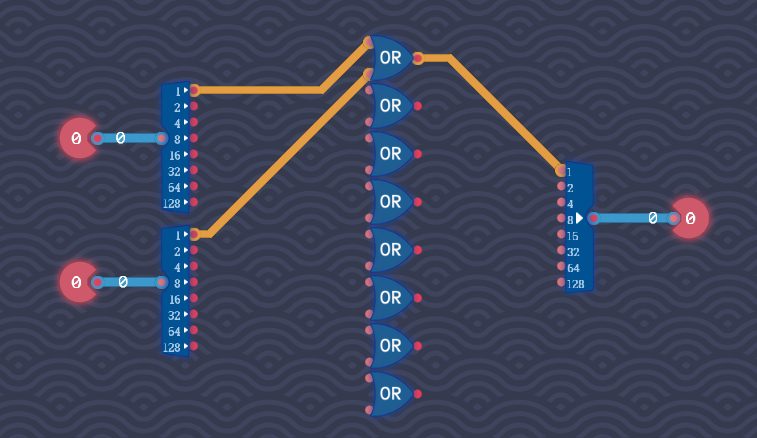
3:2桁目(2の位)から8桁目(128の位)まで配線する
ここまで来たら後は簡単です。
他の桁も同様にしてORゲートを挟んでいくだけです。
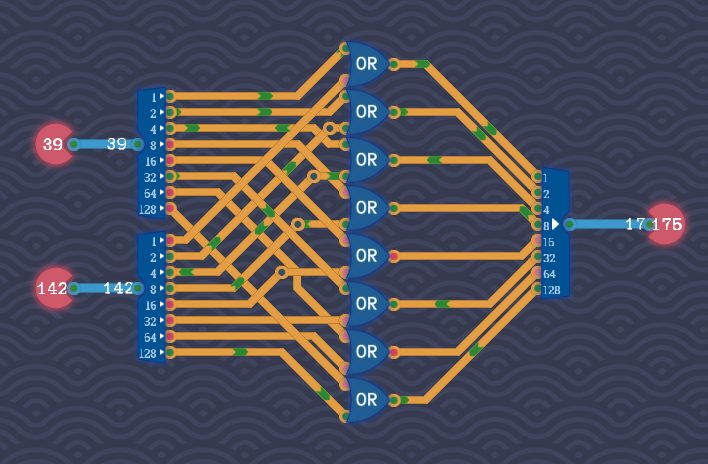
4:テストする
テストにパスすると、Byte ORコンポーネントがアンロックします。
Byte NOTステージ
Byte NOTステージのゴールは、8ビット値を反転させる回路を組むことです。
※入力値と出力値を足すと1111 1111bになります。つまり、後で解説しますが、この回路は1の補数を出力します。
【入力】
・Input ・・・8ビット
【出力】
・Output・・・8ビット


Byte NOTステージを解く
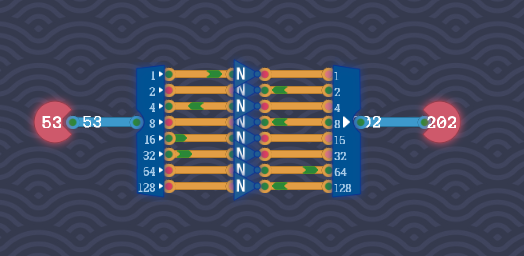
Byte Splitterコンポーネントを使って、8ビットワイヤーを1ビットごとに分離します。
各ワイヤーにNOTコンポーネントを通して、ビットを反転します。
この仕組みを全ワイヤーに適用することで、全ビットを反転できます。
後は、8 Bit Makerコンポーネントに通すだけです。
問題をクリアするとByte NOT回路がアンロックされます。
1111 1111bとXOR演算する【別解】
固定ワード長(ここでは1ワード=8ビット)の各ビットに対して論理演算をすることを、ビットごとの論理演算(bitwise operation)といいます。よく登場する演算として、次が挙げられます。
| ビットごとの論理演算の名称 | 結果 |
|---|---|
| ビットマスク | 特定のビットを残して、他を0にする。 |
| ビットセット | 特定のビットに1を設定する。それ以外はそのまま。 |
| ビット反転 | 特定のビットを反転する。それ以外はそのまま。 |
ここではビット反転について解説します。
特定のビットを反転させるには、反転したいビット部分を1にしたものと、ビットごとのXOR演算(排他的論理和)を取ります。
Byte NOTの問題では、全ビットを反転させる回路を組む必要があります。
つまり、1111 1111b(=FFh)とXOR演算しればよいことになります。
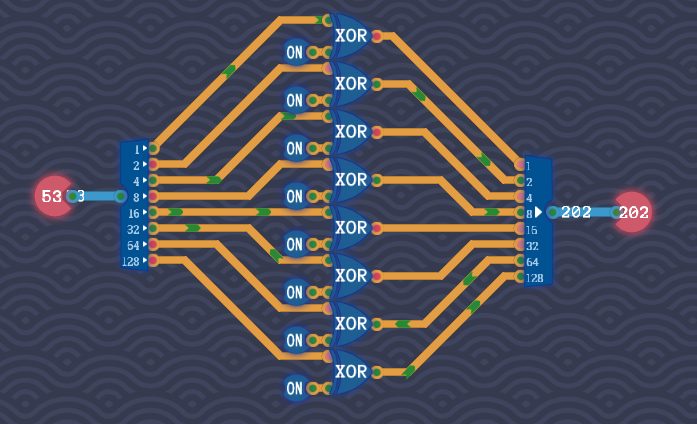
Adding Bytesステージ
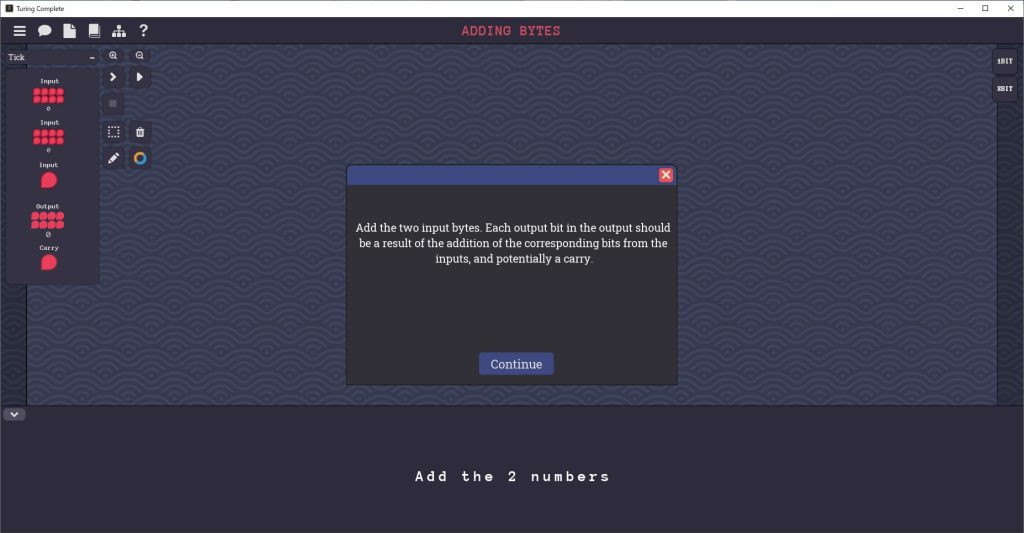
Adding Bytesステージのゴールは、2つの8ビットを加算する回路を組むことです。
【入力】
・Input・・・キャリーイン、1ビット
・Input 1・・・8ビット
・Input 2・・・8ビット
【出力】
・Output・・・8ビット
・CAR・・・キャリーアウト、1ビット
Adding Bytesステージを解く
1:設計方針を考察する
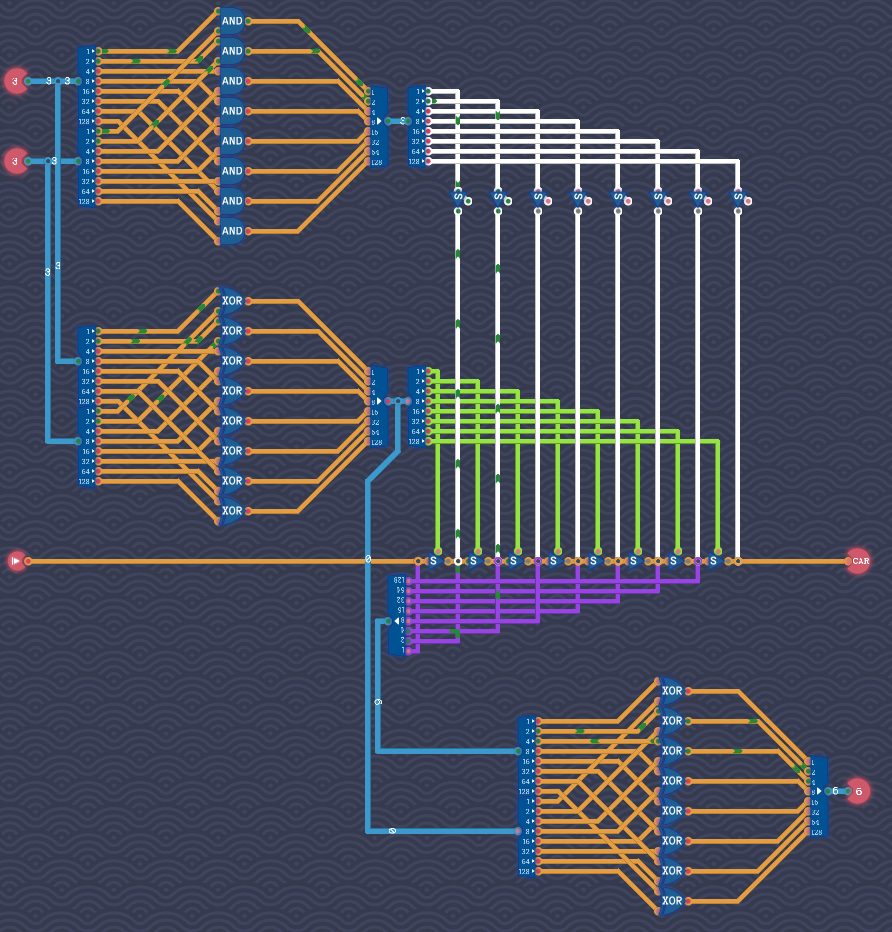
1バイト同士の加算ということは、ビット表記に変換にして、各ビットをそれぞれ加算すればよいことになります。1ビットの加算については、全加算器で実現できます。
桁上げが起きれば上位の位に加算します。回路的にいうと、下位のキャリーアウトを上位のキャリーインにつなげます。
問題は8ビットの加算がコアな回路になりますが、想像しやすいように4ビットの加算を考えてみます。
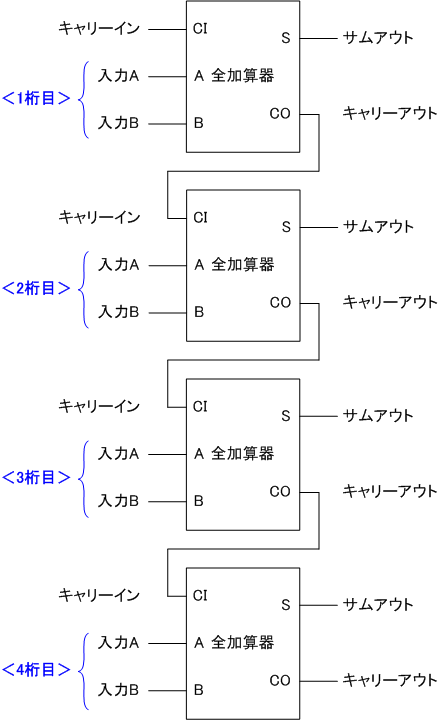
4ビット加算回路は全加算器を並列に4つ並べただけです。
以上から、8ビット加算回路でも同様にして8つ並べれば実現できると期待できます。
2:主要コンポーネントをざっくりと配置する
入力の次にByte Splitterコンポーネント、出力の手前に8 Bit Makerコンポーネントを配置します。
8桁の加算なので、中央付近にFull Adderコンポーネントを8個並列に並べます。
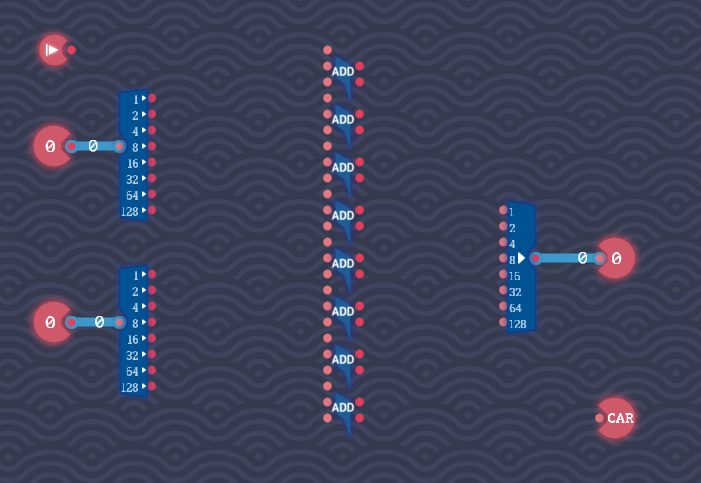
3:1桁目(1の位)に注目して回路を組む
1桁目(1の位)を加算する仕組みを実装します。1つ目のFull Adderの入出力ピンをすべて配線されればOKです。
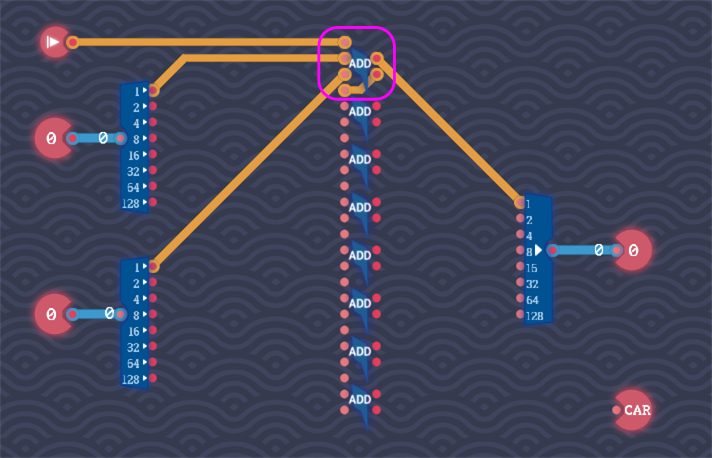
※ワイヤーの配線がしやすいように、コンポーネントの位置は各自調整してください。
4:残りの桁(2桁目~8桁目)を配線する
残りのFull Adderコンポーネントについても同様にして配線します。
配線のコツは、頭を使わずに配線できるところを先にやってしまうことです。すると、余ったピンが少なくなるため、考えるべきことが少なくなり見通しがよくなります。私の場合は、次の手順で配線しました。
①各Full Adderコンポーネントのキャリーインとキャリーアウトを先につなぎます。
②最後(8個目)のFull AdderコンポーネントのキャリーアウトはCARピンに接続します。
③各Full AdderコンポーネントのOutputと8 Bit MakerのInputをつなげます。桁が一致しており、ワイヤーを単純につなげるだけなので迷いません。
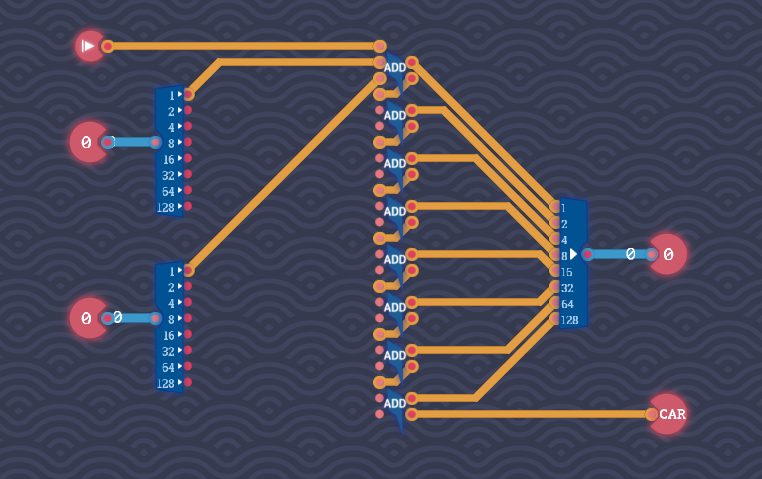
後は、Full Adderの2つのInputに、2つのByte SplitterのOutputを接続します。
※ここでは配線が見やすいように調整します。
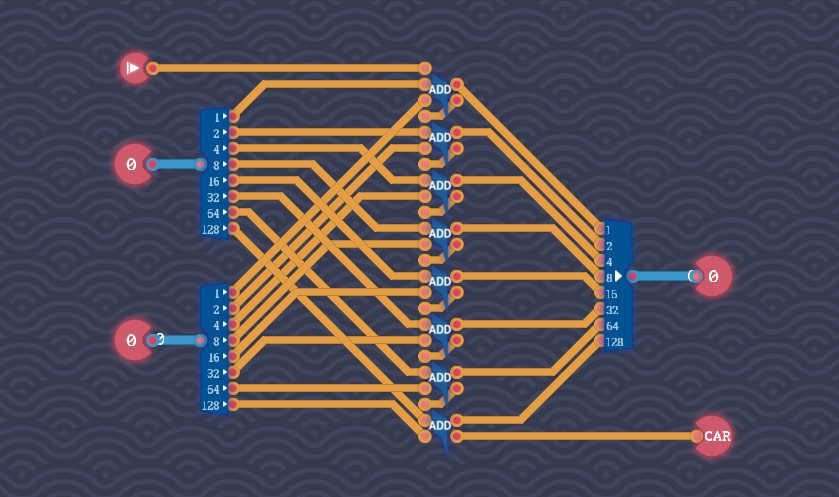
※この回路のゲートスコアは88、遅延スコアは96です。
8個のFull Adderコンポーネントがありますが、桁上がりが次々に隣の加算されています。つまり、最上位のFull Adderコンポーネントに桁上がりが到達するまでにそこそこの遅延が発生するわけです。
5:テストする
テストにクリアすると、Adding Bytesコンポーネントがアンロックされます。
1 Bit Switchコンポーネント活用する【別解】
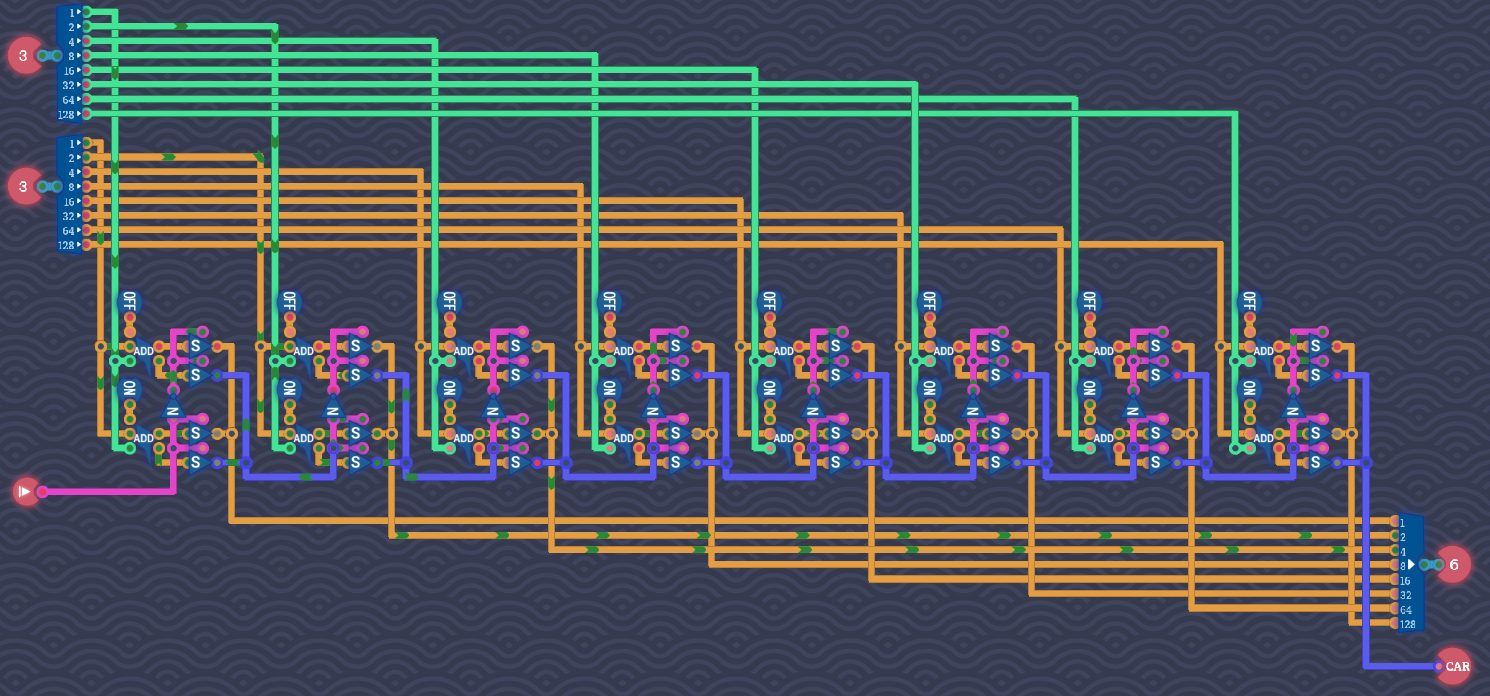
この回路のゲートスコアは216、遅延スコアは42です。
4つ組を2ペア分並べる【別解2】
8つの加算器を、4つ組の加算器が2つあるものとして考えます。ただし、キャリーインの有無で分けるので、全体として加算器が2倍に増えます。コンポーネントは増えますが、その半分は並列処理されるので、遅延スコアの改善を期待できます。
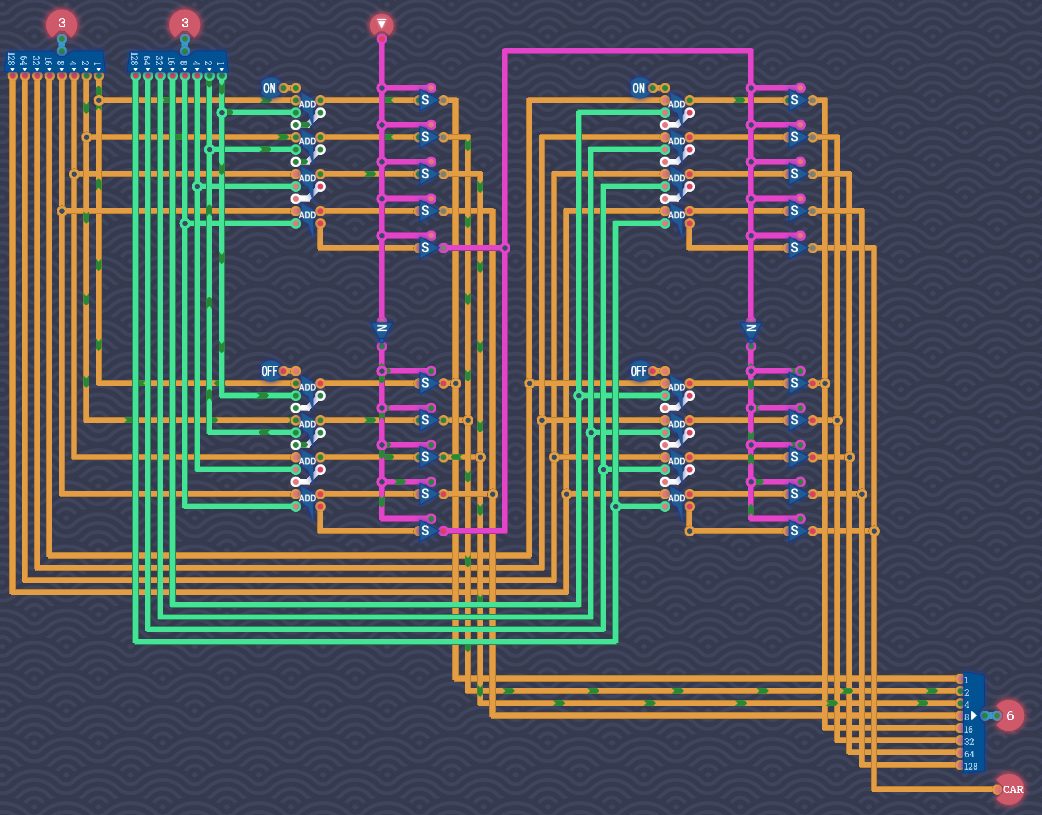
この回路のゲートスコアは198、遅延スコアは54です。
ゲートスコアは悪化しましたが、遅延スコアは改善しています。
3つ組、3つ組、2つ組を並べる【別解3】
3つ組、3つ組、2つ組に分離することで、遅延スコアが改善化します。
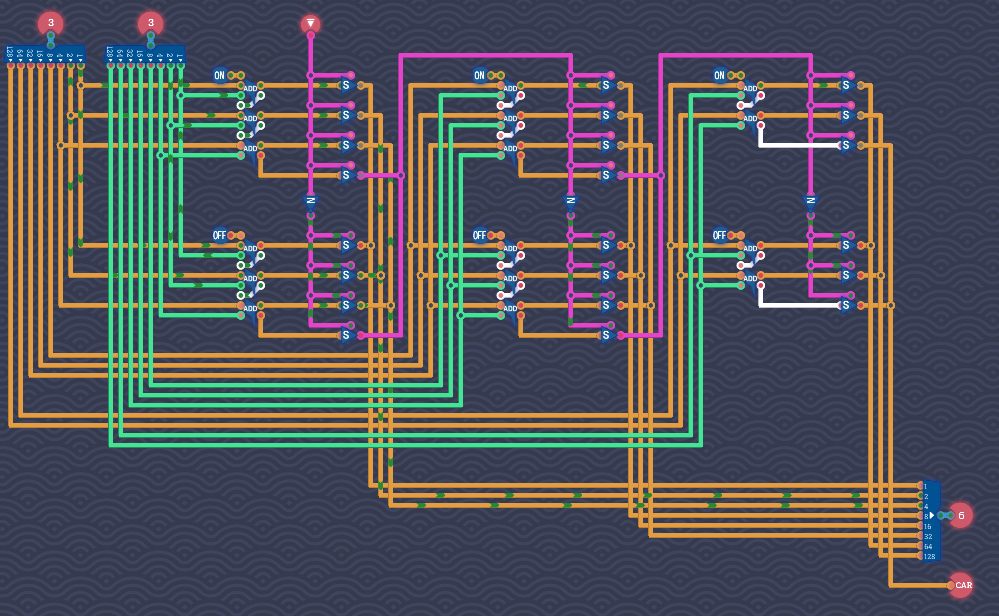
この回路のゲートスコアは201、遅延スコアは46です。
古いバージョンではこの回路で実績「Fast Adder」を解除できましたが、現バージョンでは解除できません。
2つ組を4ペア分を並べた回路にする【別解2】
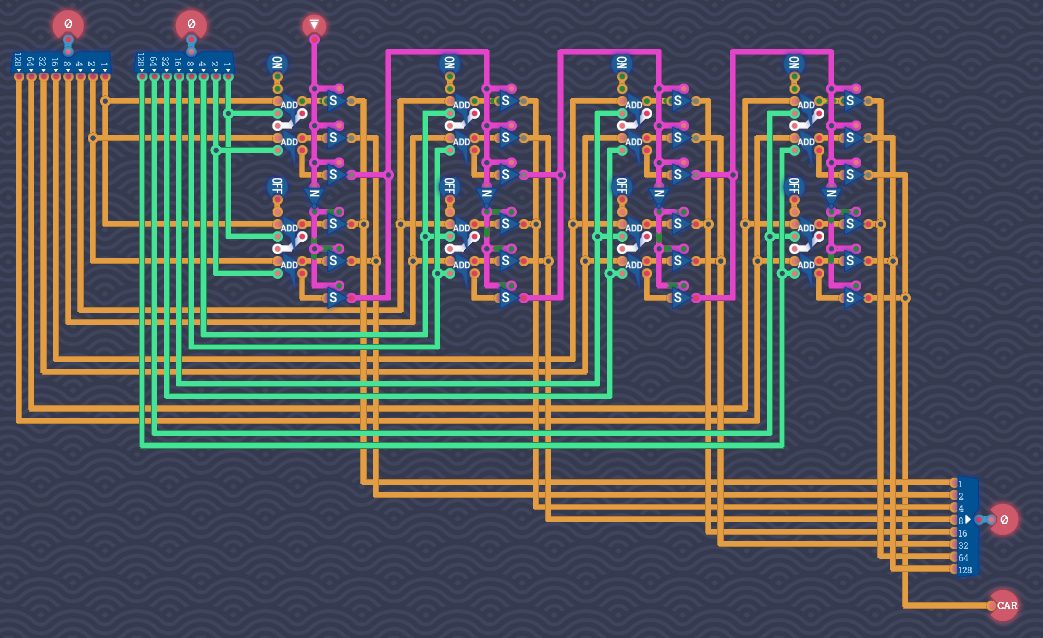
この回路のゲートスコアは204、遅延スコアは38です。
遅延スコア35以下の回路を作る【別解4】
この回路のゲートスコアは88、遅延スコアは26です。
遅延スコアは35未満なので、実績「Fast Adder」が解除されます。