Signed Less【Turing Complete編】
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
Signed Lessステージ
Signed Lessステージのゴールは、1番目の入力が2番目の入力より小さければONを出力する回路を組むことです。
ただし、入力バイトデータは符号あり(Signed)として解釈するものとします。
※Unsigned Lessステージでは符号なしの入力バイトデータを扱いましたが、本ステージでは符号ありを扱います。
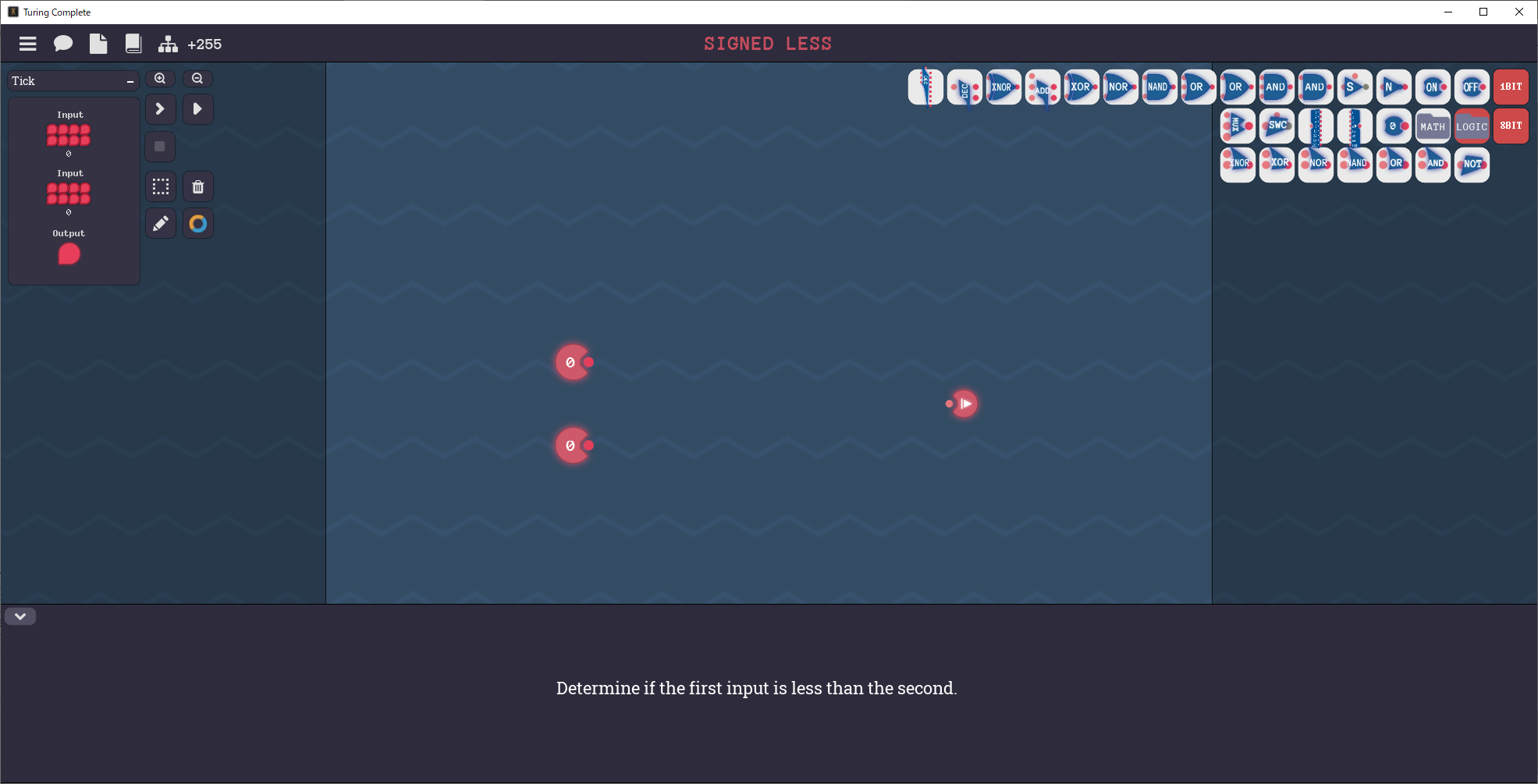
Signed Lessステージを解く
1:ナンバーフォーマットを符号ありに切り替える
ナンバーフォーマットを切り替えるアイコンを押して「-1」にしておきます。これでテスト時に10進数が負の数が表示されるようになります。
※この設定はあくまで表示のためであり、回路が正しければステージはクリアできます。ただし、この設定をしておけば、回路の挙動を理解するための助けになります。
2:回路の設計を検討する
最上位ビットが0であれば、Unsigned Lessステージの回路のままで、本ステージのゴールを満たします。
問題は最上位ビットが1のときになります。最上位ビットが1であれば、-128から-1までのいずれかの値を取ります。
最上位ビットだけ1のビット列、すなわち1000 0000bとXOR演算するというテクニックを採用します。
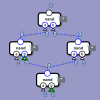
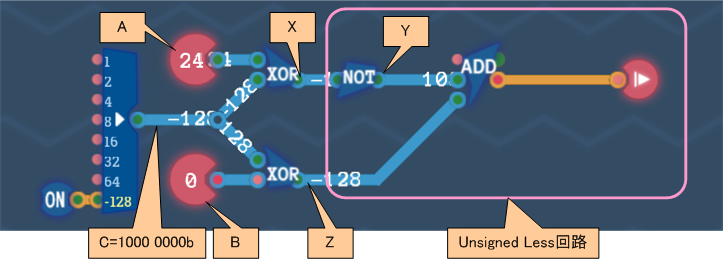
天下り的ですが、次のような回路を考えます。Unsigned Less回路の前段に、2入力とも1000 0000bとXORする回路が組み込まれています。
Aは上のInput端子のビット列、Bは下のInput端子のビット列、C=1000 0000bとします。
XORの性質から、$a \, \text{XOR} \, 0 =a, \, a \, \text{XOR} \, 1 = \bar{a}$が成り立ちます。ただし、$a, \, b \in \{0, \,1\}$とします。
Cは最上位が1、それ以外の桁が0と固定であることを考慮します。
すると、X(=XOR(A, C))とZ(=XOR(C, B))は、最上位(1桁のみ)だけがビット反転し、他の桁は変化しません。
一方、Y(=NOT(X))はXのビット反転です。言い換えると、最上位だけが変化せず、他の桁はビット反転します。
| ケース | A | B | X | Y | Z | Add(Y, Z)のCarry Outピン | Add(Y, Z)のResultピン |
|---|---|---|---|---|---|---|---|
| A=B | 0110 0110b (=102d) | 0110 0110b (=102d) | 1110 0110b | 0001 1001b | 1110 0110b | 0 | 1111 1111b |
| A=B | 1000 1001b (=119d) | 1000 1001b (=119d) | 0000 1001b | 1111 0110b | 0000 1001b | 0 | 1111 1111b |
| A>B | 0110 0110b (=102d) | 0001 1101b (=29d) | 1110 0110b | 0001 1001b | 1001 1101b | 0 | 1011 0110b |
| A>B | 1111 0000b (=-16d) | 1001 0101b (=-107d) | 0111 0000b | 1000 1111b | 0001 0101b | 0 | 1010 0100b |
| A<B | 0010 0001b (=33d) | 0101 1100b (=92d) | 1010 0001b | 0101 1110b | 1101 1100b | 1 | 0011 1010b |
| A<B | 1110 0011b (=-29) | 1111 0000b (=-16) | 0110 0011b | 1001 1100b | 0111 0000b | 1 | 0000 1100b |
※最上位ビットが1なら負の数であり、負の数のケースもカバーするようにしました。
確かに「A<B」のケースのみで、出力がONになっています。
※証明したわけではなく、具体的な数値からの予想であり、一般化を期待できます。より具体例をたくさん試すのは、シミュレーターのテストに任せることにします。なお、この時点で予想外であれば、テスト以前の問題であり、回路の設計が間違っていることになります。
3:回路を実装する
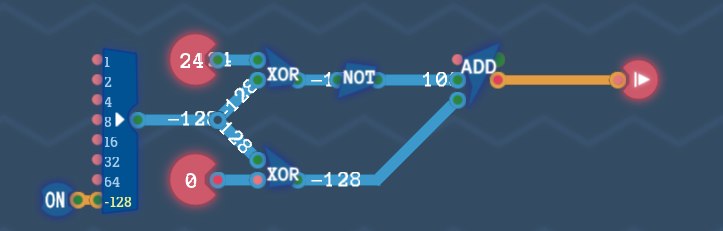
回路を組むと次のようになります。
ちなみに、XORコンポーネントとNOTコンポーネントのセットは、XNORコンポーネントに置き換えられます。

4:テストする
クリアすると、Signed Lessコンポーネントをアンロックします。
入力の最上位ビットに注目した回路を組み込む【別解】
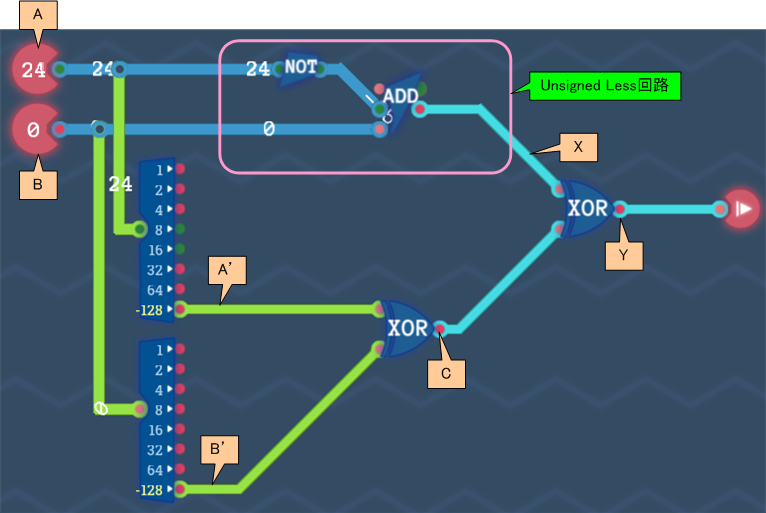
Aは上のInput、Bは下のInputとします。C、Xを回路の中間状態、Yを出力値とします。
次に示す4パターンに分類します。
| ケース | パターン |
|---|---|
| ① | 「Aが正」かつ「Bが正」[1]ここでいう正とはゼロ以上を意味するものとします。 |
| ② | 「Aが正」かつ「Bが負」 |
| ③ | 「Aが負」かつ「Bが正」 |
| ④ | 「Aが負」かつ「Bが負」 |
[1]ケース①の場合
Unsigned Lessステージと同じ状況なので、「A<B」のときにXはON(=1)になります。
AとBが正ということは、A’=B’=0です。
C=XOR(A’, B’)=XOR(0, 0)=0 【確定】
XORの公式$a \, \text{XOR} \,0=a$により、Yは「A<B」のときにONになります。
よって、本ステージのゴールを満たします。
[2]ケース②の場合
必ず「A>B」であり、本ステージのゴールを満たすには出力は0でなければなりません。
Aが8 Bit NOTコンポーネントを通過した時点で、最上位ビットは1になります。Bは最初から最上位ビットが1です。これら2つのビット列をADD演算すると必ず桁上がりが発生します。つまり、Carry Outピンが1、すなわちX=1になります。
Aが正、Bが負ということは、A’=0、B’=1になります。
C=XOR(A’, B’)=XOR(0, 1)=1 【確定】
XORの公式$a \, \text{XOR} \, 1= \bar{a}$により、$Y=\bar{X}=\bar{1}=0$になります。
確かに0を出力することを確認できました。
[3]ケース③の場合
必ず「A<B」であり、本ステージのゴールを満たすには出力は1でなければなりません。
Aが8 Bit NOTコンポーネントを通過した時点で、最上位ビットは0になります。Bは最初から最上位ビットは0です。これら2つのビット列をADD演算すると必ず桁上がりが発生しません。つまり、Carry Outピンが0、すなわちX=0になります。
Aが負、Bが正ということは、A’=1、B’=0になります。
C=XOR(A’, B’)=XOR(1, 0)=1 【確定】
XORの公式$a \, \text{XOR} \, 1= \bar{a}$により、$Y=\bar{X}=\bar{0}=1$になります。
確かに1を出力することを確認できました。
[4]ケース④の場合
負の数の世界では、(最上位ビットを除いて)上位のビットがONであれば、より大きい値になります。
※正の数の世界と同じになります。
例えば、1100 0000b=-64、1010 0000b=-96
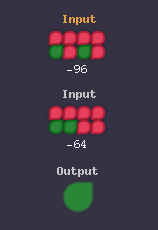
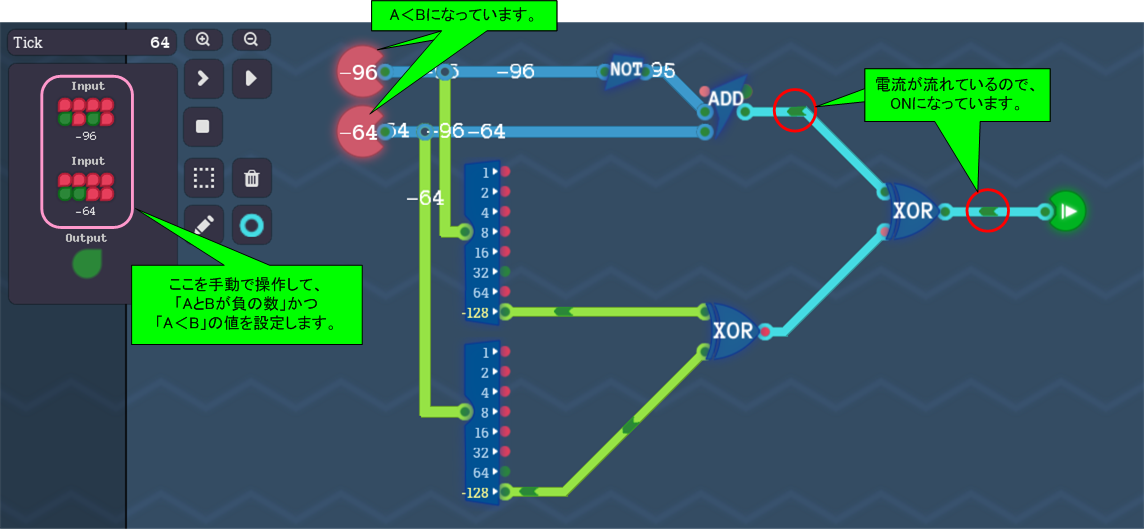
つまり、Unsigned Less回路に対して2つの負の数を入力に与えても、「A<B」のときにXはON(=1)になります。
ところで、AとBが負ということは、A’=B’=1です。
C=XOR(A’, B’)=XOR(1, 1)=0 【確定】
XORの公式$a \, \text{XOR} \,0=a$により、Yは「A<B」のときにONになります。
よって、本ステージのゴールを満たします。
ゆえに、すべてのケースにおいて、ゴールを満たすので、この回路はSigned Less回路になることがわかります。
もう少し複雑にしたバージョン【別解2】
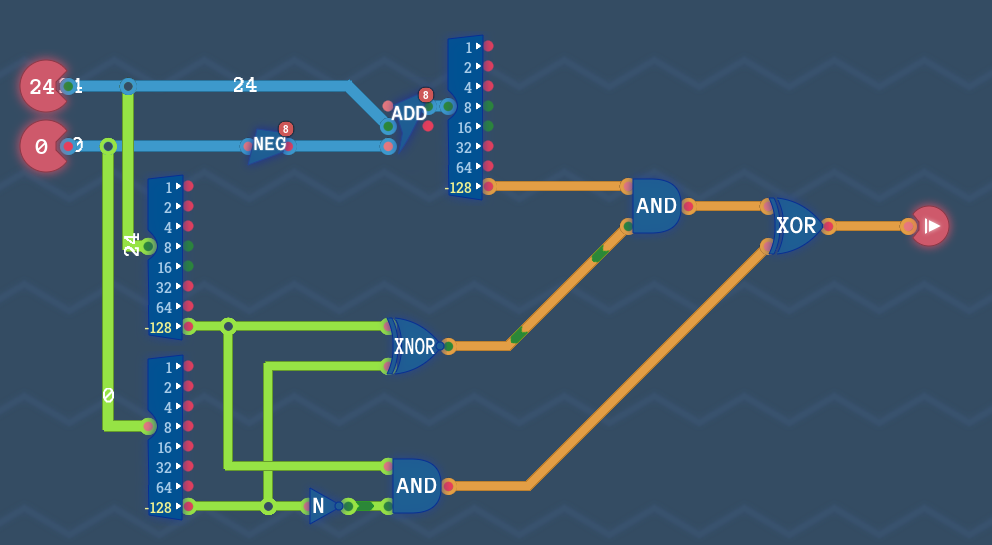
References
| ↑1 | ここでいう正とはゼロ以上を意味するものとします。 |
|---|