Unsigned Less【Turing Complete編】

2023年9月7日

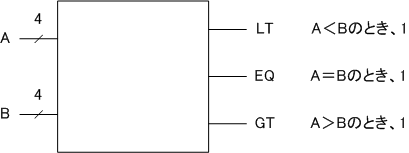
大小比較器

大小比較器（マグニチュードコンパレーター）とは、2つ入力を比較して、どちらが大きいか、あるいは等しいかを判定する回路です。

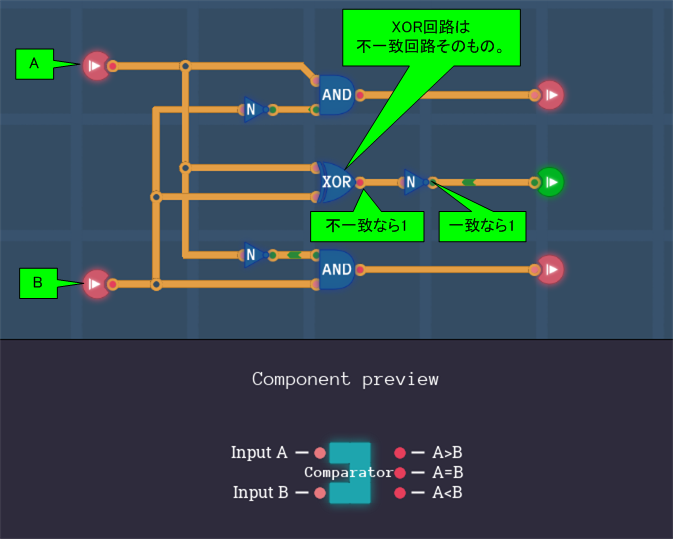
1ビット大小比較器

1ビットの入力が2つあり、その大小を識別する回路です。

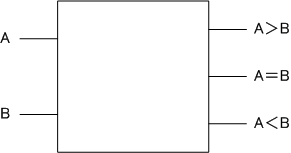
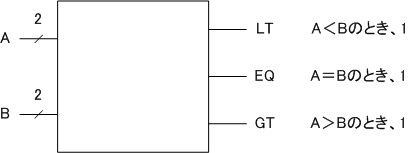
真理値表

A	B	A=B	A＜B	A＞B
0	0	1	0	0
0	1	0	1	0
1	0	0	0	1
1	1	1	0	0

デジタル回路

※AとBに関係するラインを色分けしました。

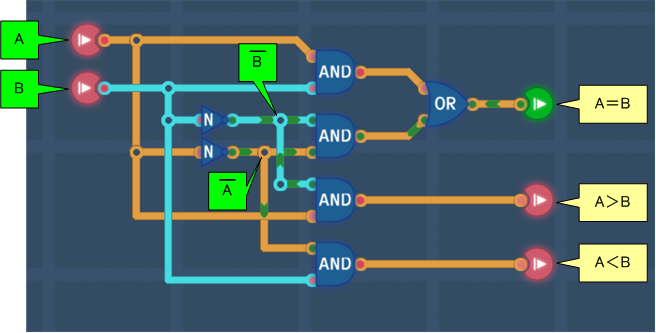
若干複雑に見えます。これはA=Bのときに1を出力する回路が「2つのANDゲート＋ORゲート＋2つのNOTゲート」と多数の拭くゲートを組み合わせているためです。この回路は一致回路であり、不一致回路と等価であるXORゲートとNOTゲートを組み合わせた回路に置き換えられます。

XOR回路にNOTゲートを追加してもよいのですが、XOR回路の内部構成によってはすでに出力直前にNOTゲートを使って折り、その際はこれを取り除けばよいのです。

以上を踏まえて回路を書き換えると次のようになります。回路の意味が明確になり、ワイヤリングもすっきりしています。

※Component previewにピンがすべて表示されるように、入力端子を離して配置しました。またわかりやすいようにラベル名も設定しています。

2ビット大小比較器

2ビットの入力が2つあり、その大小を識別する回路です。

A=A2A1、B=B2B1とします。

論理式

それぞれの出力の論理式がわかれば、基本論理素子で回路を組めます。

LTの論理式

A<Bの場合は、次の2通りに分けられる。

(a) A2＜B2のとき

A2=0かつB2=1

$LT1 = \overline{A2} \cdot B2$

(b)「A2=B2」かつ「A1＜B2」

$LT2 = \overline{A2 \oplus B2} \cdot ( \overline{A1} \cdot B1)$

※$\oplus$はXORを意味します。XORしてからNOTを取っているというXNORです。XORは不一致回路であることを思い出してください。不一致回路を反転させると一致回路ということです。

したがって、

$LT=LT1 + LT2$

EQの論理式

A=Bの場合は、「A2=B2」かつ「A1＝B1」のときになります。

$EQ= \overline{A2 \oplus B2} \cdot \overline{A1 \oplus B1} $

GTの論理式

A＞の場合は、次の2通りに分けられます。

(a)A2＞B2のとき

$GT1 = A2 \cdot \overline{B2}$

(b)「A2=B2」かつ「A1＞B2」のとき

$GT2= \overline{A2 \oplus B2} \cdot (A1 \cdot \overline{B1})$

したがって、

$GT=GT1 + GT2$

デジタル回路

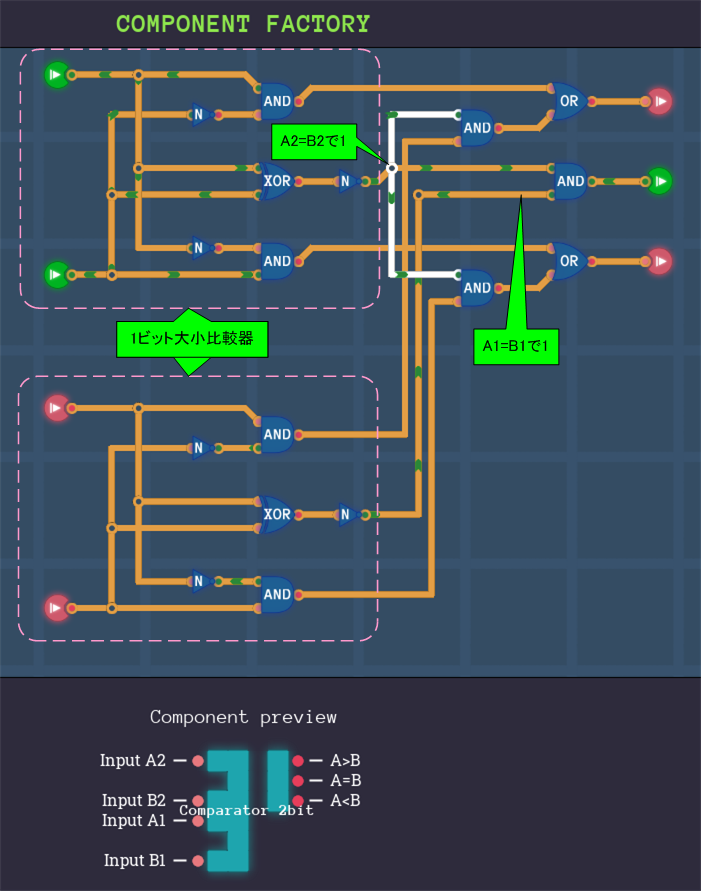
自然と拡張版1ビット大小比較器が得られた

2ビット大小比較器は1ビット大小比較器を2つ組み合わせることで構築できました。

次のように破線で囲んだ回路を考えます。すると、対称とする桁の入力と下位の桁からの判定結果に対して、全体の判定結果を出力する回路になっています。この回路を拡張版1ビット大小比較器と名づけます。

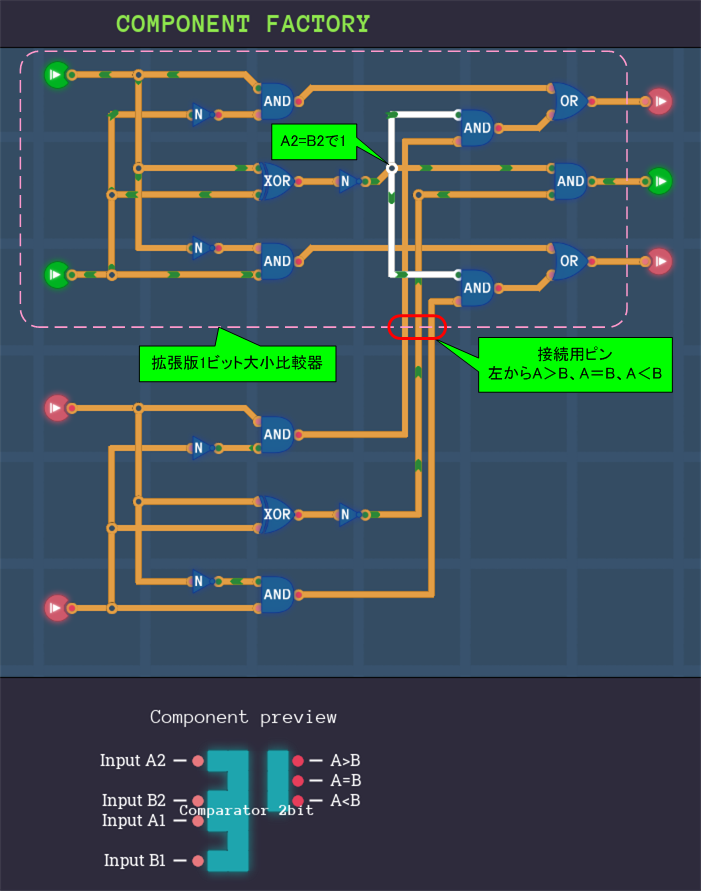
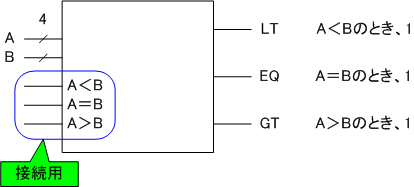
拡張版1ビット大小比較器を標準として作っておくといろいろと便利です。右上の部分の回路を考える必要がなくなるのです。

2つ並べてつなげれば2ビット大小比較器になりますし、3つ並べてつなげれば3ビット大小比較器になります。ただし、最下位に対応する拡張版1ビット大小比較器の接続用ピンについては、初期入力として「A>B」ピンを0、「A=B」ピンを1、「A<B」ピンを0とします。

変形版2ビット大小比較器

通常の大小比較器は3つのケースそれぞれの出力がありました。

状況によっては、それぞれのケースを識別するのではなく、特定のケースのみに1を出力させたいことがあります。

※例えば、Unsigned Lessステージで組む回路もそうです。

「A=B」のときに1を出力するのであれば、一致回路なので、XNORそのものです。

問題は「A＜B」か「A＞B」のときになります。今回は「A＜B」のときについて解説しますが、「A＞B」についても一般性を失いません。

4ビット大小比較器

4ビットの入力が2つあり、その大小を識別する回路です。

A=A4A3A2A1、B=B4B3B2B1とします。

2ビット大小比較器から4ビット大小比較器を構築する

作りたい回路は上記の4ビット大小比較器です。

[1]最上位2桁A4A3とB4B3の比較

2ビット大小比較器を使って、入力としてA4A3とB4B3を与えます。

3つの出力を次のように定義します。

[2]最上位2桁A2A1とB2B1の比較

[1]と同様に次のように定義します。

[3]最終的な出力を決定する

・LTが1になるには、LT_upper or 「EQ_upperかつLT_lower」

・EQが1になるには、EQ_upperかつEQ_lower

・GTが1になるには、GT_upper or「EQ_upperかつGT_lower」

4ビット大小比較器の内部構成は次のようになります。

同様なやり方で、4ビット大小比較器から8ビット大小比較器を構築できます。これは一般化できます。

2ⁿビット大小比較器から、2ⁿ⁺¹ビット大小比較器を構築できるのです。

今までの構築例について、nに注目してみます。

・1ビット（＝2⁰）大小比較器から2（＝2⁰⁺¹）大小比較器

・2ビット（＝2¹）大小比較器から4（＝2¹⁺¹）大小比較器

・4ビット（＝2²）大小比較器から8（＝2²⁺¹）大小比較器

8ビット大小比較器

拡張版4ビット大小比較器から8ビット大小比較器を構築する

接続用の入力を備えた、拡張版4ビット大小比較器を考えます。

これを2つ使って、8ビット大小比較器を構築するには、次のように接続するだけです。

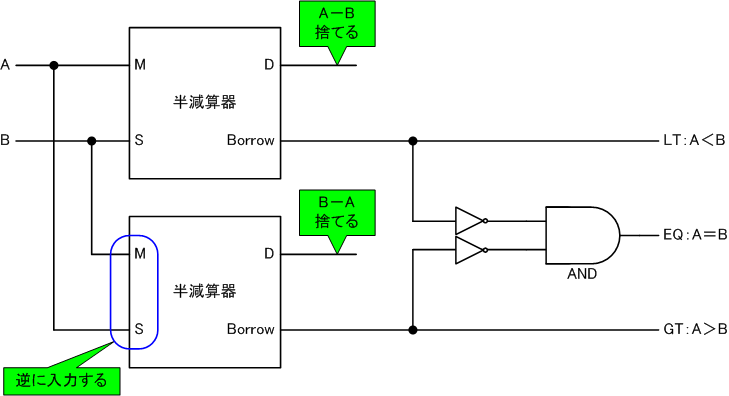
半減算器から大小比較器を作る

半減算器の入出力については、以下のWebページを参照ください。

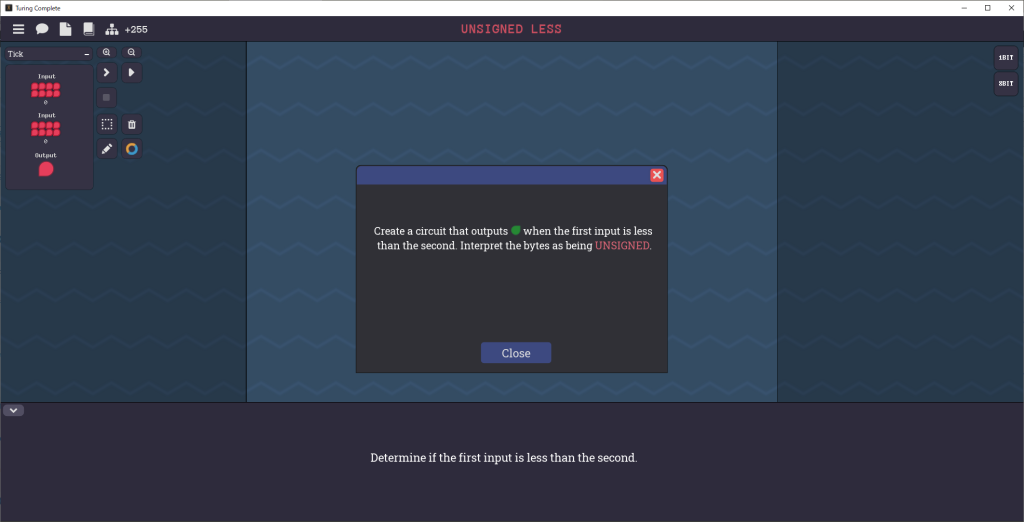
Unsigned Lessステージ

Unsigned Lessステージのゴールは、1番目の入力が2番目の入力より小さければONを出力する回路を組むことです。

ただし、入力バイトデータは符号なし（Unsigned）として解釈するものとします。

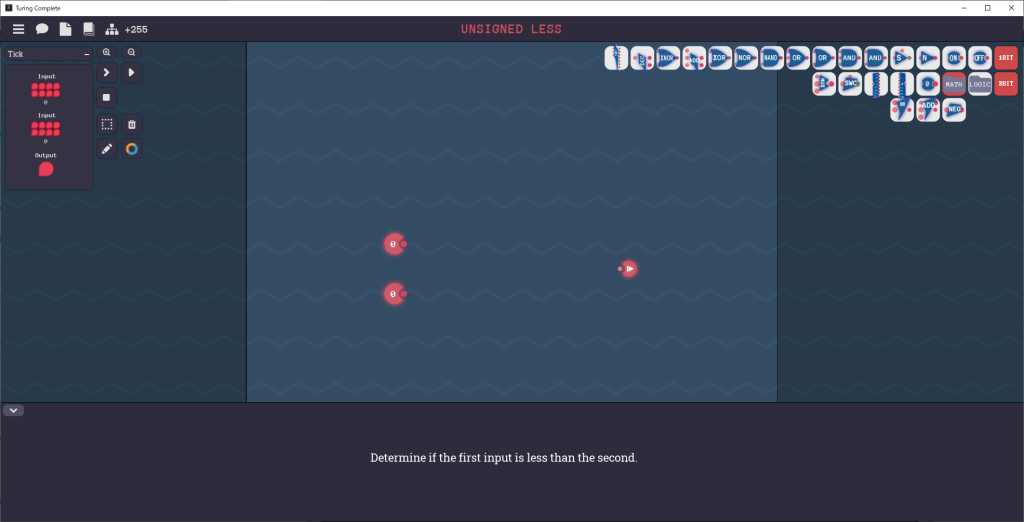
Unsigned Lessステージを解く

1：回路の設計を検討する

Equalityステージの別解で紹介した、前段の回路を見てください。

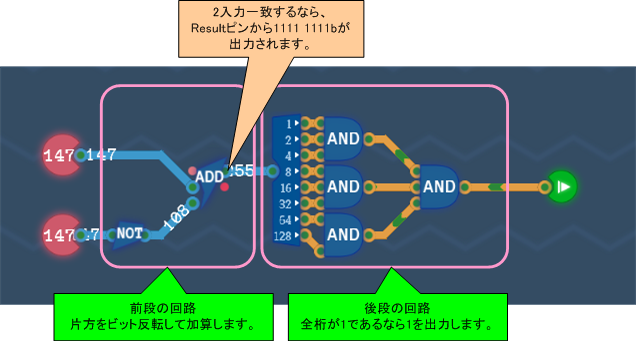
本ステージでは一致ではなく、大小を識別することになります。

大小を識別する基本戦略は、減算してゼロより大きいか小さいかを調べることになります。

8ビット用の減算コンポーネントはありません。

※ALUコンポーネントは減算をサポートしていますが、本ステージでは使えません。

AとBについて3つのパターンが考えられます。具体的なビット列で、Addの出力結果がどう変わるのかを確認してみます。Carry Outピンに注目するのがポイントです。

ケース	A（上のInput端子）	B（下のInput端子）	￣B（Bのビット反転）	Add(A, ￣B)のCarry Outピン	Add(A, ￣B)のResultピン
A=B	0110 0110b	0110 0110b	1001 1001b	0	1111 1111b
A>B	0110 0110b	0001 1101b	1110 0010b	1	0100 1000b
A<B	0010 0001b	1001 1100b	0110 0011b	0	1000 0100b

本ステージは「A<B」を確定的に知りたいわけですが、残念ながらCarry Outピンに注目しても「A<B」のケースを確定できません。

なぜなら0になるのは「A<B」だけでなく「A=B」のケースも含まれるためです。

※逆に「A>B」を識別する回路は、前段の回路をそのまま流用して、出力端子に接続すれば実現できます。

しかし、この考察は無駄ではありません。前段の回路を少し変更を加えれば、うまくいきそうであることがわかります。それは、下のInput端子側の8 Bit NOTコンポーネントを外して、代わりに上のInput端子側に配置するのです。

以上の考察を踏まえて、回路を組むと次のようになります。

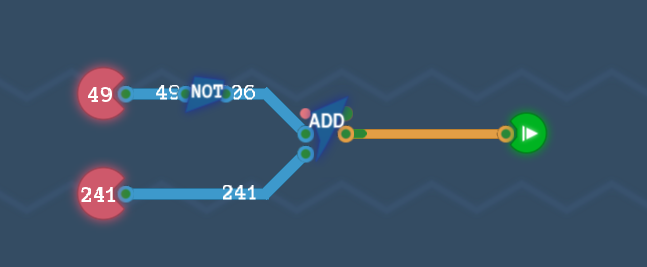
実際にテストする前に、表を使って手計算で確認してみます。

ケース	A（上のInput端子）	B（下のInput端子）	￣A（Aのビット反転）	Add(￣A, B)のCarry Outピン	Add(￣A, B)のResultピン
A=B	0110 0110b	0110 0110b	1001 1001b	0	1111 1111b
A>B	0110 0110b	0001 1101b	1001 1001b	0	1011 0110b
A<B	0010 0001b	1001 1100b	1101 1110b	1	0111 1010b

Carry Outピンが1になるのは、「A<B」のケースのみです。つまり、Carry Outピンに注目することで、「A<B」を識別できるわけです。

2：回路を実装する

シミュレーター上に、上記に示した修正版回路（上に8 Bit NOTコンポーネントがある回路）を組んでください。

3：テストする

クリアすると、Unsigned Lessコンポーネントがアンロックします。