Odd Number of Signals【Turing Complete編】

2023年8月16日2023年9月16日

Odd Number of Signals

4入力のうち奇数個がONなら、出力をONにする回路を組みます。

4入力、1出力の回路。

使用できるコンポーネントは最大3つまでという条件がついています。

※3種類ではなく、3つまで。

「4入力＝入力が4ビット」であるため、真理値表には16パターン（＝2⁴）の状態があります。

奇数判定回路

Turing Completeの問題は、4入力のうちTが奇数個であればTを出力するという回路を作るというものです。

つまり、奇数を判定する回路を作ることになります。

以降、奇数判定回路を呼ぶことにします。

4入力なので、4入力型の奇数判定回路です。

奇数判定回路の設計方針

たくさん入力がある場合は、少ない本数から考察し、1本ずつ入力を増やす回路に拡張してきました。

今回もその方針を採用します。

1入力型の奇数判定回路

「1入力のうちTが奇数個であれば、Tを出力する」回路は、入力がTかどうかの回路、すなわちそのまま出力すればよいことになります。

バッファーゲート、あるいはワイヤーそのものです。

2入力型の奇数判定回路

「2入力のうちTが奇数個であれば、Tを出力する」回路を考えます。

これは真理値表を書いてしまうのが一番簡単です。

a	b	Output
F	F	F
F	T	T
T	F	T
T	T	F

aかbのどちらかがTのときだけ、Tを出力しています。

この真理値表はどこかで見たことがあるはずです。そうです。XORゲートの真理値表そのものです。

つまり、XORゲートは2入力型の奇数判定回路といえます。

真理値表から論理式を求めると次の通りになります。式を展開していくと、やはりaとbの排他的論理和になります。

$Output=~\bar{a}~\cdot~b~+~a~\cdot~\bar{b} =a~\oplus~b$

3入力型の奇数判定回路

2入力型の奇数判定回路（XORゲート）を再活用できないかを考えます。

3入力のうち2本をXORゲートに通せば、この2本について奇数の判定済みです。

残りの1本は未判定ですが、1入力型の奇数判定回路を通したと考えられます。なぜなら、1入力の奇数判定回路はワイヤーと同等だからです。

以上で判定済みの2本が得られます。

ところで、判定結果を奇数判定回路に通しても、判定が正しく動作します。

回路にまとめると次のようになります。

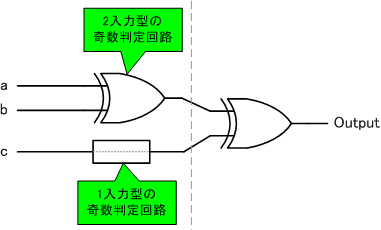
Odd Numbers of Signalsステージを解く

ここまで来ればもう簡単です。

4入力型の奇数判定回路を作りましょう。

XORゲートをカスケード接続していくだけで奇数判定回路を構成できることが判明しました。

4入力型になっても同様です。むしろ3入力型より簡単に気づきやすいかもしれません。

一気に作ってしまいましょう。

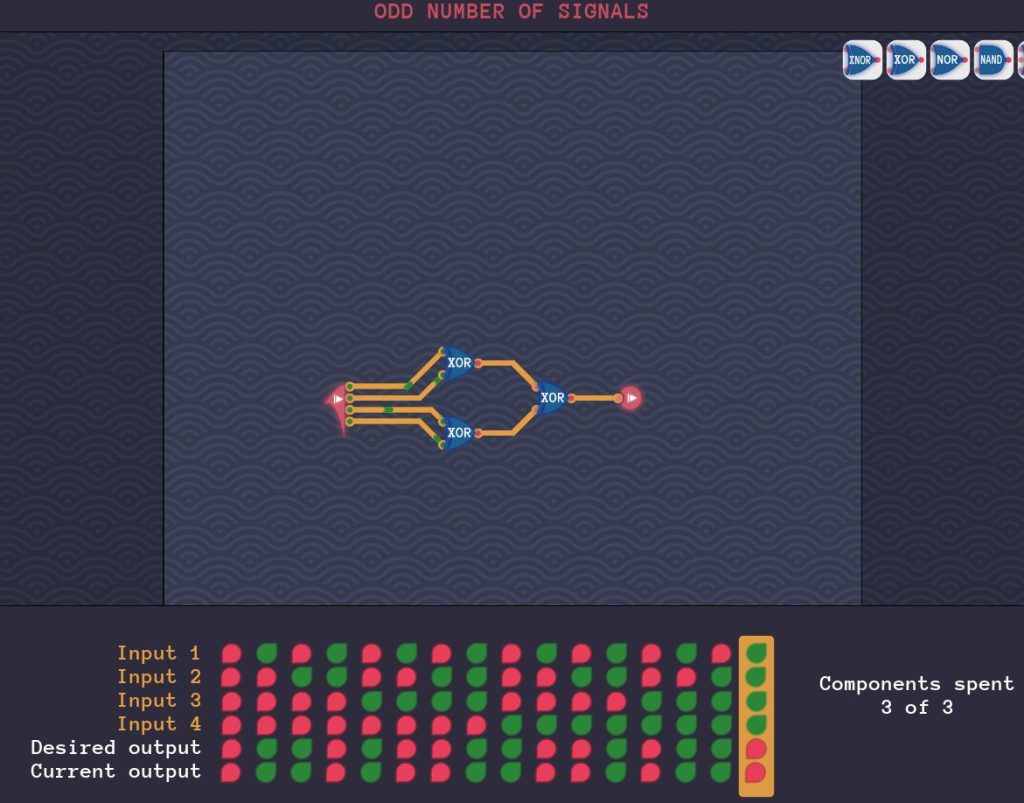
3つのコンポーネントだけという条件も満たしています。

XOR回路のつなげかたを変える【別解】

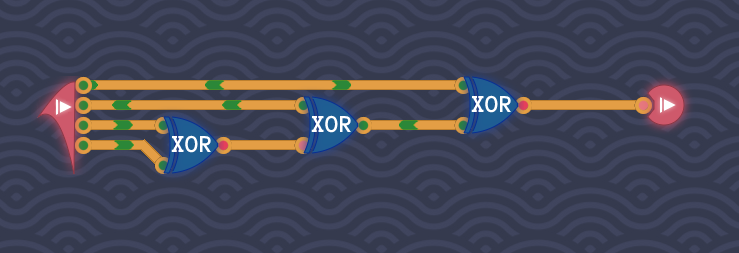
奇数判定回路から偶数判定回路へ

n入力型の奇数判定回路の作り方を習得しました。

偶数判定回路を必要な場合は、奇数判定回路から簡単に作れます。

偶数判定は奇数判定の逆になるだけなので、出力を反転させるためにNOTゲートを通すだけです。

奇数判定回路は偶数パリティ発生器そのもの

パリティチェック方式

パリティチェック方式は、データにパリティビットと呼ばれる1ビットの検査用ビットを付加して、ビット列から1ビットの誤りを検出する方式です。

パリティビットを付加する際に、「1」のビット数の合計を偶数にする方式を偶数パリティ、「1」のビット数の合計を奇数にする方式を奇数パリティといいます。

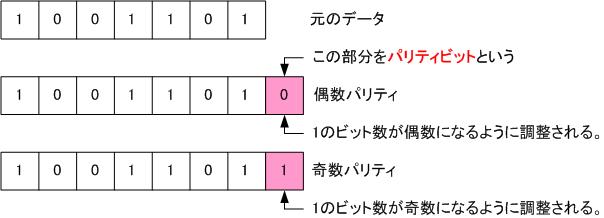
例えば、送信者は「1001101」を偶数パリティでデータを送信したとします。

このとき偶数パリティ値は0であり、伝送路を「10011010」が移動します。

データ伝送の際にノイズなどで1ビット反転してしまい、結果として受信者に「11011010」が到達したものとします。

あらかじめ偶数パリティを使っていると送信者と受信者で決めていましたのので、受信者は受信データ「11011010」を調べます。すると、「1」のビット数が5個あり、偶数ではないので、おかしいと検知できます。つまり途中で何らかのビット反転（あるいはビット欠損）があったと判断できるので、送信者にもう一度同じものを送信してくれるように要求します。

パリティ発送回路

パリティ発生回路とは、パリティビット（パリティチェック用のビット）を生成する回路です。パリティ発生器（パリティジェネレーター）とも呼ばれます。

ソフトウェアでも実現できるが、ハードウェアの論理演算回路で作る方法を紹介します。

（4ビット入力の）偶数パリティ発生回路

ブロック図

入力	出力
・IN[3:0]･･･4ビット	・EVEN_OUT･･･1ビット 偶数パリティビット IN[3:0]における1の個数が偶数⇒EVEN_OUT=0 IN[3:0]における1の個数が奇数⇒EVEN_OUT=1

奇数判定回路は1の個数が奇数なら、出力が1でした。これは偶数パリティ発生回路と同じ入出力であり、同じ構成で作れるということです。

真理値表

IN[3]	IN[2]	IN[1]	IN[0]	EVEN_OUT
0	0	0	0	0
0	0	0	1	1
0	0	1	0	1
0	0	1	1	0
0	1	0	0	1
0	1	0	1	0
0	1	1	0	0
0	1	1	1	1
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	1
1	1	1	0	1
1	1	1	1	0

論理式

単純に論理式を求めると次のようになります。

$$EVEN\_OUT=~IN_3~IN_2~IN_1~\bar{IN_0}~+~IN_3~IN_2~\bar{IN_1}~IN_0~+~IN_3~\bar{IN_2}~IN_1~IN_0~+~IN_3~\bar{IN_2}~\bar{IN_1}~\bar{IN_0}~+~\bar{IN_3}~IN_2~IN_1~IN_0~+~\bar{IN_3}~IN_2~\bar{IN_1}~\bar{IN_0}~+~\bar{IN_3}~\bar{IN_2}~IN_1~\bar{IN_0}~+~\bar{IN_3}~\bar{IN_2}~\bar{IN_1}~IN_0$$

$=(~IN_3~IN_2~IN_1~\oplus~IN_0~)~+~(~IN_3~\oplus~IN_2~IN_1~IN_0~)~+~(~IN_1~\oplus~IN_3~IN_2~IN_0~)~+~(~IN_2~\oplus~IN_3~IN_1~IN_0~)$

$=IN_0~\oplus~(~IN_1~\oplus~(~IN_2~\oplus~IN_3~)~)$　←(*)

カルノー図が市松模様の場合、出力の論理式はすべての入力をExORまたはExNORしたものです。

カルノー図の左上角が0なので、ExORを用います。

この方法を使えば、上記の方法よりも簡単に論理式を得られます。

$EVEN\_OUT=IN_3~\oplus~IN_2~\oplus~IN_1~\oplus~IN_0$　←(**)

(*)の括弧を取れば、(**)と同時になります。

（4ビット入力の）奇数パリティ発生回路

ブロック図

入力	出力
・IN[3:0]･･･4ビット	・ODD_OUT･･･1ビット 奇数パリティビット IN[3:0]における1の個数が奇数⇒ODD_OUT=0 IN[3:0]における1の個数が偶数⇒ODD_OUT=1