電気フェンスの最適化【The Signal State編】
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
電気フェンスの最適化(Electric Fence Optimization)
SRC1からは一連のランダムな値が出力されます。
SRC1の値が5の倍数だった場合、それをOUT1に出力してください。
SRC1の値が2の倍数だった場合、それをOUT2に出力してください。
SRC1の値が②の倍数かつ5の倍数だった場合、それをOUT3に出力してください。
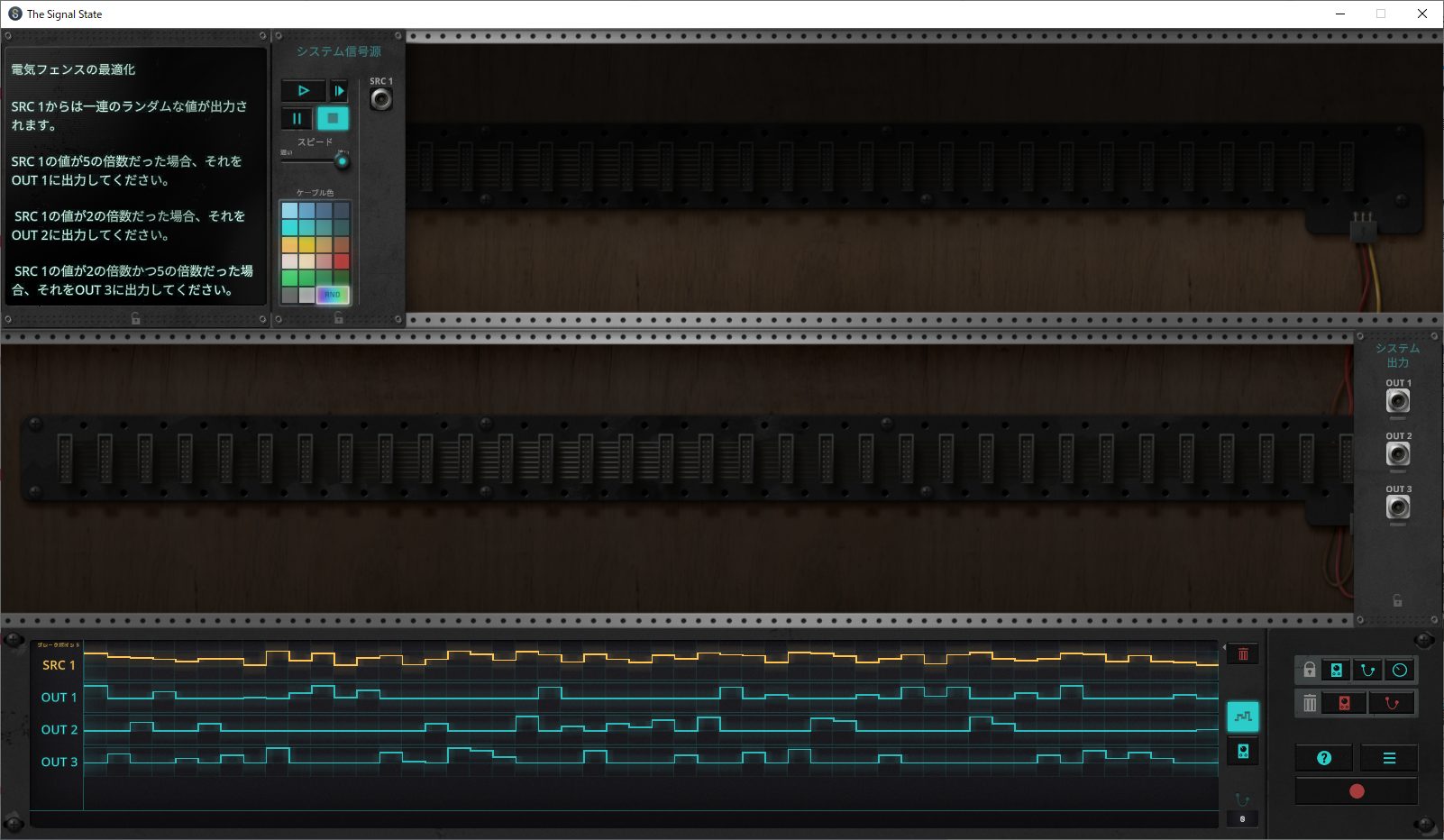
ゴールを確認する
SRC1が2の倍数や5の倍数かどうかによって、出力先が変わります。
出力先が3つあるので、SRC1は3パターンあると間接的にわかりますが、きちんと分類しておきます。
「2の倍数は偶数そのもの」「偶数と奇数は同時に満たさない」「表における○は満たす、×は満たさないを意味する」であることを留意してください。
| 2の倍数 | 5の倍数 | SRC1の数値例 | 出力先 |
|---|---|---|---|
| × | × | 1、3、7、11、39、77 ※5の倍数ではない奇数 | 指示されていない。 ※テストパターンではこれに該当するSRC1は使われない。 |
| × | ○ | 5、15、25、55,85 | OUT1 |
| ○ | × | 2、4、16、72 | OUT2 |
| ○ | ○ | 10、20、30、100 | OUT3 |
0はすべての倍数になりえますが、The Signal Stateのシステム的には該当しないようです。もしそうなら、出力先が不明になります。
電気フェンスの最適化を解く
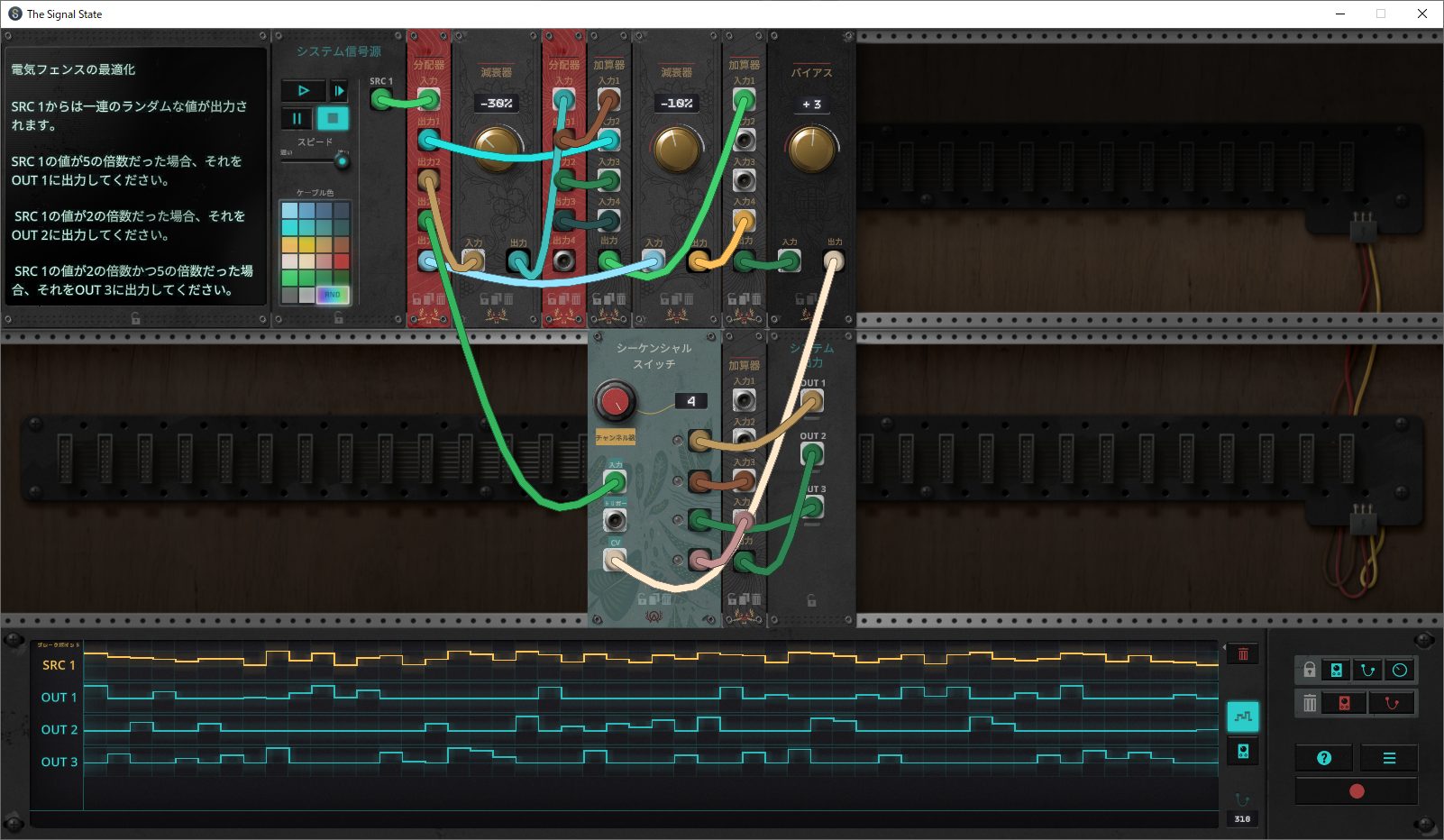
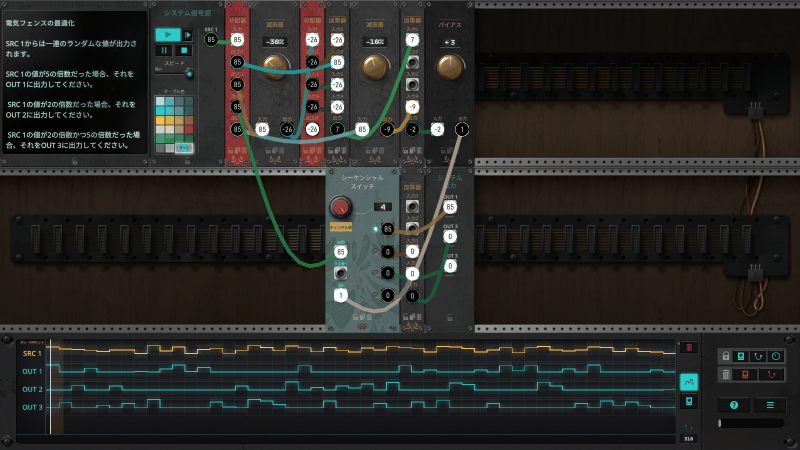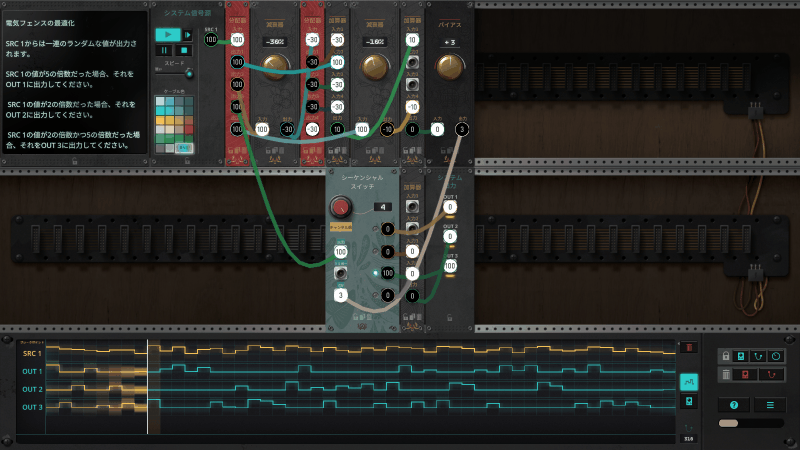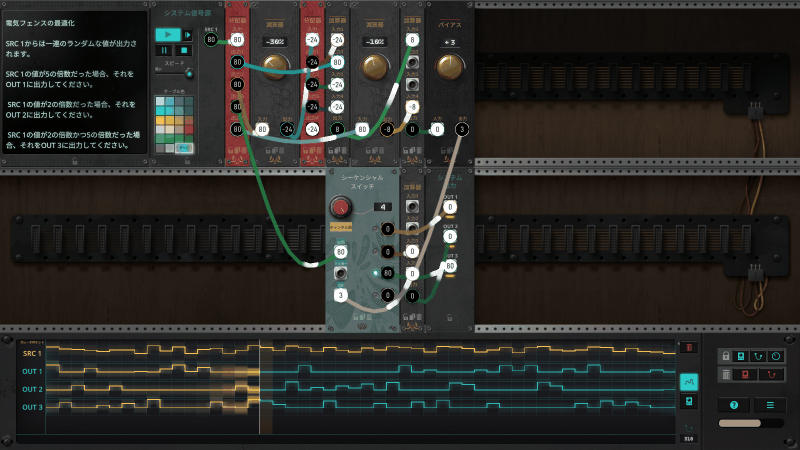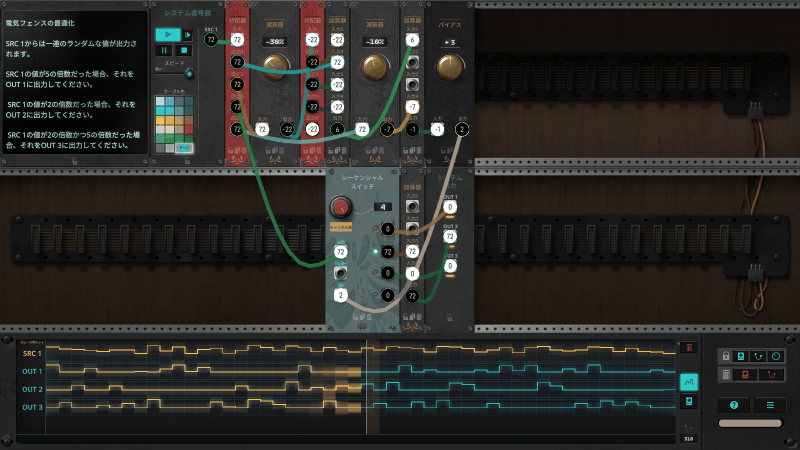
回路の挙動をトレースする
個人的に複雑な仕組みであるように感じたため、1ステップずつ実行して(序盤の)挙動を確認してみました。
[1]SRC1=85の場合
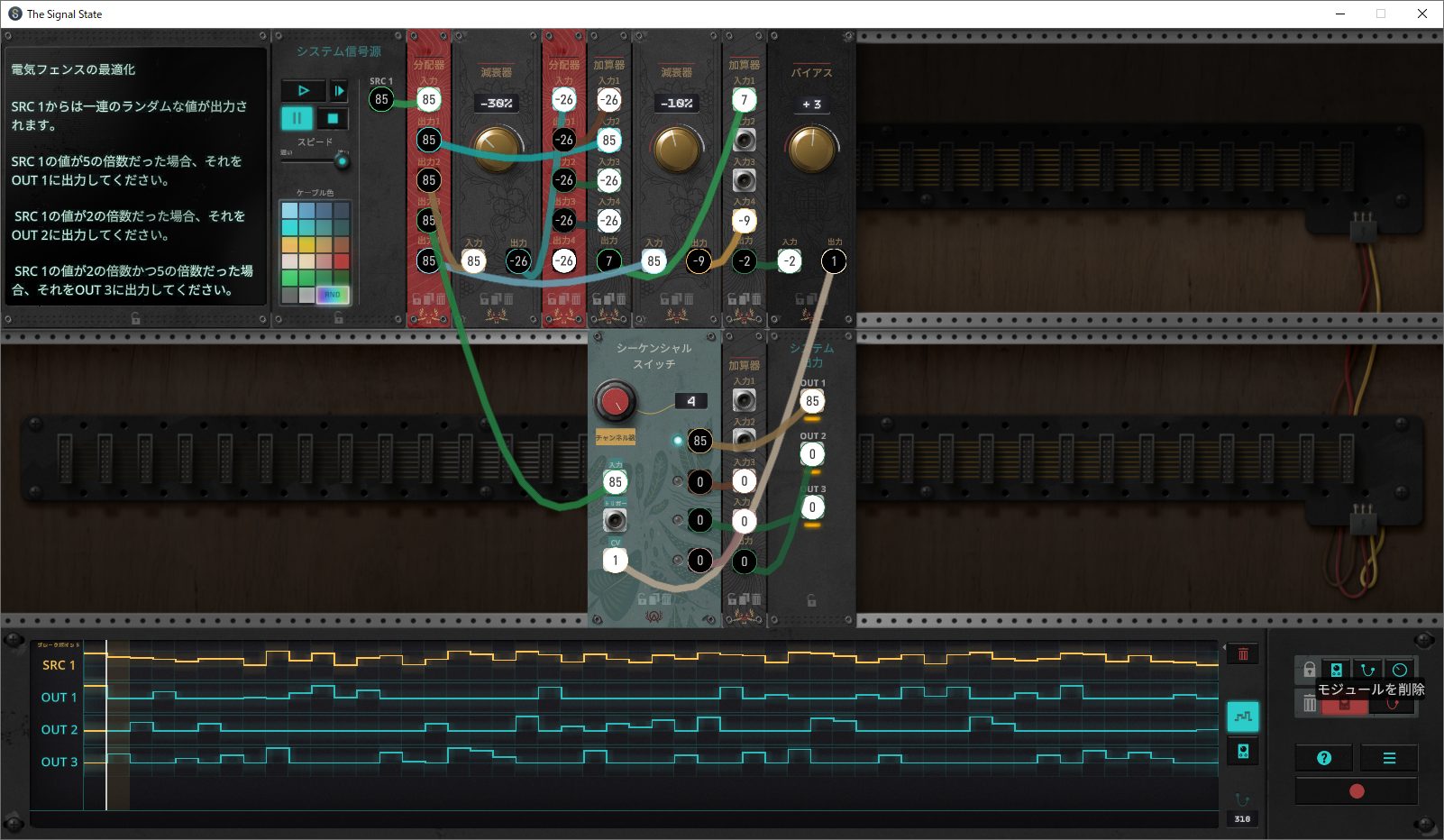
上のラック上の回路は、シーケンシャルスイッチモジュールのCVに与える電圧値を求めています。
システムをデバッグすると、小数点以下で四捨五入し、常に整数を扱っているようです。
(間違っていたらすみません)
負の数の場合でも、近い整数が選択されています。
ところで、-1.5の四捨五入は-1か-2かという議論がありますが、ここではExcelのROUND関数と同様だと感じました。
ROUND(-1.5)=2になります。
このシステムでも、「-8.4⇒-8」「-8.5⇒-9」でした。
ここで、SRC1=x、yは上のラックの右から2番目の加算器モジュールから出力される電圧値、zはシーケンシャルスイッチモジュールのVCに入力される電圧値とします。
$$y=ROUND\Big( x \times – \frac{30}{100} \Big) +ROUND\Big( x \times – \frac{30}{100} \Big) + ROUND \Big( x \times – \frac{30}{100} \Big) + x$$
$$z=ROUND\Big( x \times – \frac{10}{100} \Big) +y+3$$
それでは実際に計算してみます。画像の数字と一致していることも確認してください。
$$y=ROUND\Big( 85 \times – \frac{30}{100} \Big) +ROUND\Big( 85 \times – \frac{30}{100} \Big) + ROUND \Big( 85 \times – \frac{30}{100} \Big) + 85$$
$$=ROUND\Big( -25.5 \Big) +ROUND\Big( -25.5 \Big) + ROUND \Big( -25.5 \Big) + 85$$
$$=-26 -26 -26 + 85$$
$$=7$$
$$z=ROUND\Big( 85 \times – \frac{10}{100} \Big) +7+3$$
$$=ROUND\Big( -8.5 \Big) +7+3$$
$$=-9 +7+3$$
$$=1$$
計算すると、z=1になります。
よって、チャンネル1が選ばれ、OUT1に85が出力されます。
確かにSRC1は5の倍数であり、OUT1への出力でつじつまがあいます。
[2]SRC1=x=60の場合
$$y=ROUND\Big( 60 \times – \frac{30}{100} \Big) +ROUND\Big( 60 \times – \frac{30}{100} \Big) + ROUND \Big( 60 \times – \frac{30}{100} \Big) + 60$$
$$=ROUND\Big( -18 \Big) +ROUND\Big( -18 \Big) + ROUND \Big( -18 \Big) + 60$$
$$=-18-18-18 + 60$$
$$=6$$
$$z=ROUND\Big( 60 \times – \frac{10}{100} \Big) +6+3$$
$$=-6+6+3$$
$$=3$$
よって、チャンネル3が選ばれ、OUT3に60が出力されます。
※60は2の倍数でもあり5の倍数でもあります。
[3]SRC1=x=56の場合
$$y=ROUND\Big( 56 \times – \frac{30}{100} \Big) +ROUND\Big( 56 \times – \frac{30}{100} \Big) + ROUND \Big( 56 \times – \frac{30}{100} \Big) + 56$$
$$=ROUND\Big( -16.8 \Big) +ROUND\Big( -16.8 \Big) + ROUND \Big( -16.8 \Big) + 56$$
$$=-17 -17-17+ 56$$
$$=5$$
$$z=ROUND\Big( 56 \times – \frac{10}{100} \Big) +5+3$$
$$=ROUND\Big( -5.6 \Big) +5+3$$
$$=-6+5+3$$
$$=2$$
よって、チャンネル2が選ばれ、OUT3に56が出力されます。
[4]SRC1=x=45の場合
$$y=ROUND\Big( 45 \times – \frac{30}{100} \Big) +ROUND\Big( 45 \times – \frac{30}{100} \Big) + ROUND \Big( 45 \times – \frac{30}{100} \Big) + 45$$
$$=ROUND\Big( -13.5 \Big) +ROUND\Big( -13.5 \Big) + ROUND \Big( -13.5 \Big) + 45$$
$$=-14 -14-14+ 45$$
$$=3$$
$$z=ROUND\Big( 45 \times – \frac{10}{100} \Big) +3+3$$
$$=ROUND\Big( -4.5 \Big) +3+3$$
$$=-5+3+3$$
$$=1$$
よって、チャンネル1が選ばれ、OUT1に45が出力されます。
※以降については、各自調べてみてください。


