Counting Signals【Turing Complete編】

2023年8月17日2023年9月16日

Counting Signalsステージ

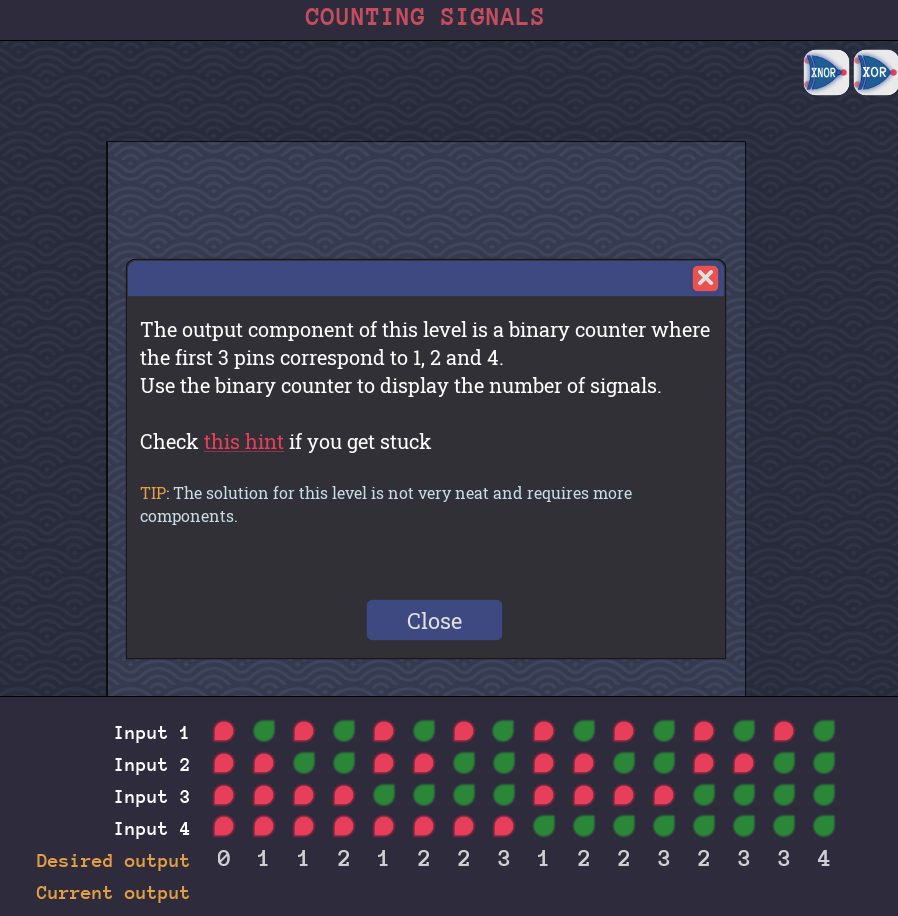
Counting Signalsステージのゴールは、4つの入力のうち、ONになっている個数を2進数で出力させる回路を作ることです。

Counting Signalsステージを解く

1：設計方針を検討する

4ビット入力、3ビット出力。

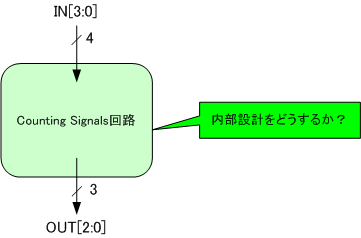
入力の4ビットは0000b～1111bのパターンがあります^[1]bは2進数値を強調する印です。。

※Tと1、Fと0が対応するものとしています。

出力の3ビットは000b～100bのパターンがあります。なぜなら、入力が全部ONだったとすれば、出力は100b（＝4d）であるためです^[2]dは10進数値を強調する印です。。

真理値表から論理式を求めてもよいのですが、手間がかかります。

そこで、出力は3ビットであり、各桁を出力する回路を別々に設計することにします。

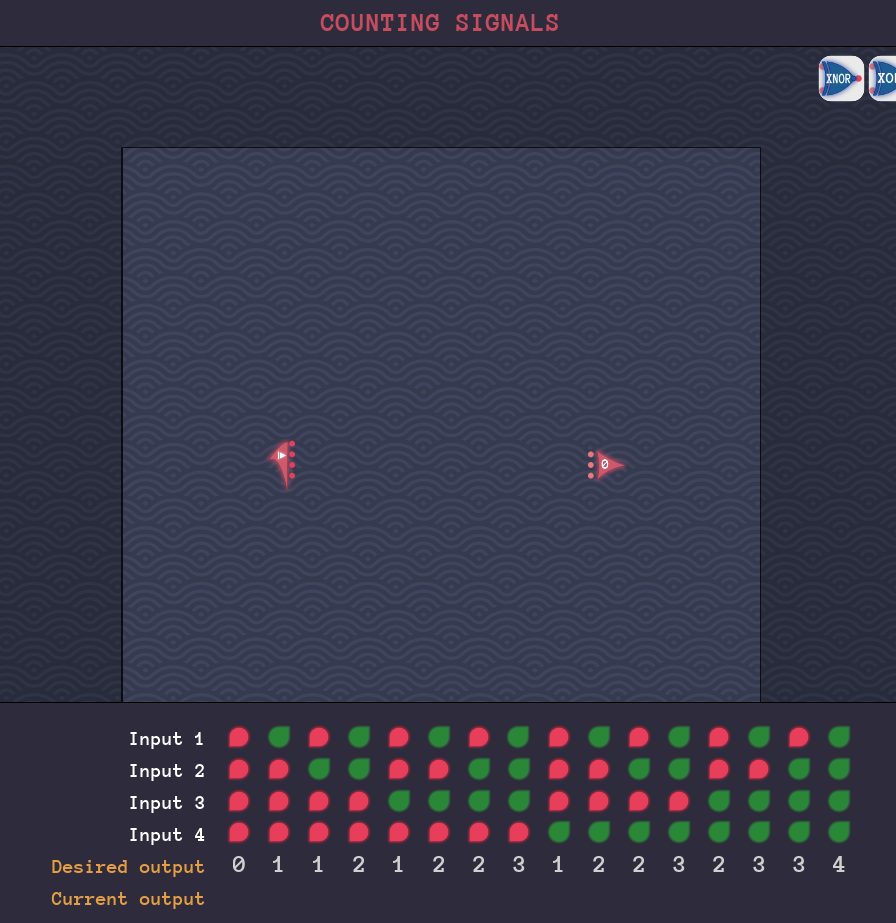
2：接続しやすいようにワイヤーを並べる

3：出力の4の位を生成する回路を設計する

OUT2がTになるのは、全入力がTのときだけです。

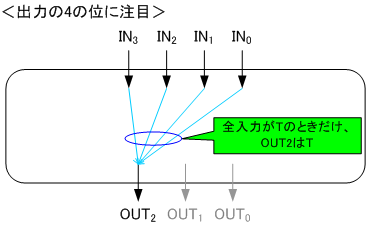
つまり、INの4つの矢印を4入力型ANDゲートの入力につなげればよいことになります。

ただし、手元に4入力型ANDコンポーネントがないので、3入力型ANDコンポーネントとANDコンポーネントで代用します。

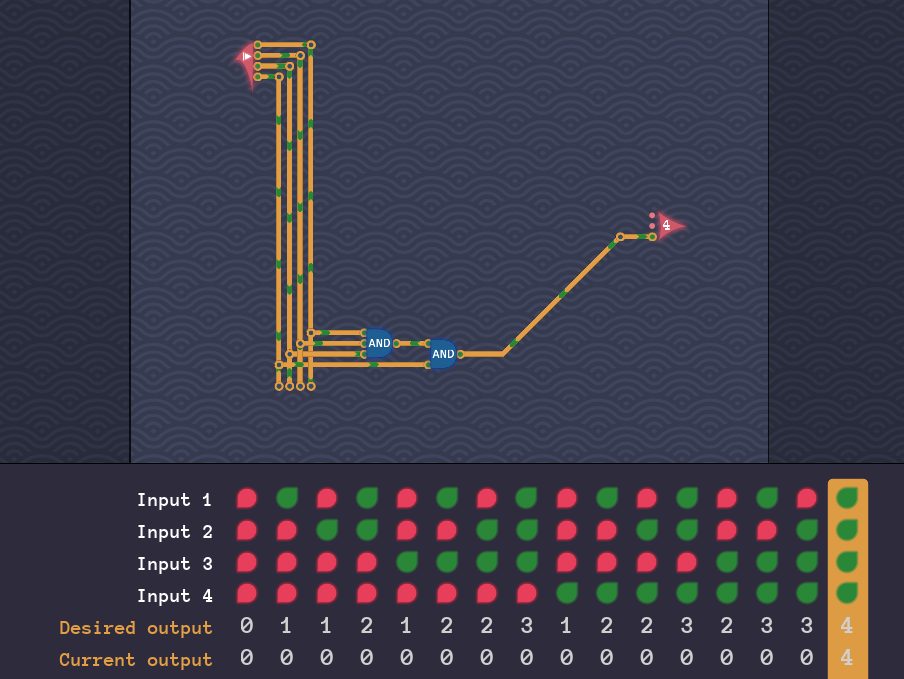
4の位についてだけテストしておきます。

[Run]ボタンを押すと2の位と1の位につながる回路を組んでいないのでエラーになります。[Next]ボタンを押して、一番右の（全入力がON）のところが4を出力してパスすることをチェックします。

4：出力の1の位を生成する回路を設計する

順番的には2の位に注目すべきですが、ここは一番難しいので後回しにして、先に1の位に注目します。

出力の1の位がTになるのは、入力のTが奇数個のときのみです。

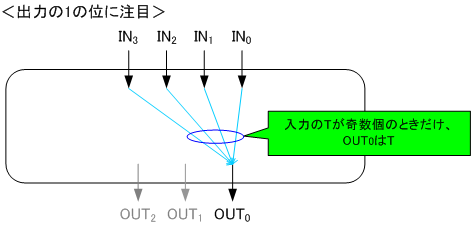
つまり、奇数判定回路の出力を1の位につなげればよいことになります。

入力は4つなので、4入力型の奇数判定回路を用います。これはすでにOdd Number of Signalsの問題で作成済みです。これを流用します。

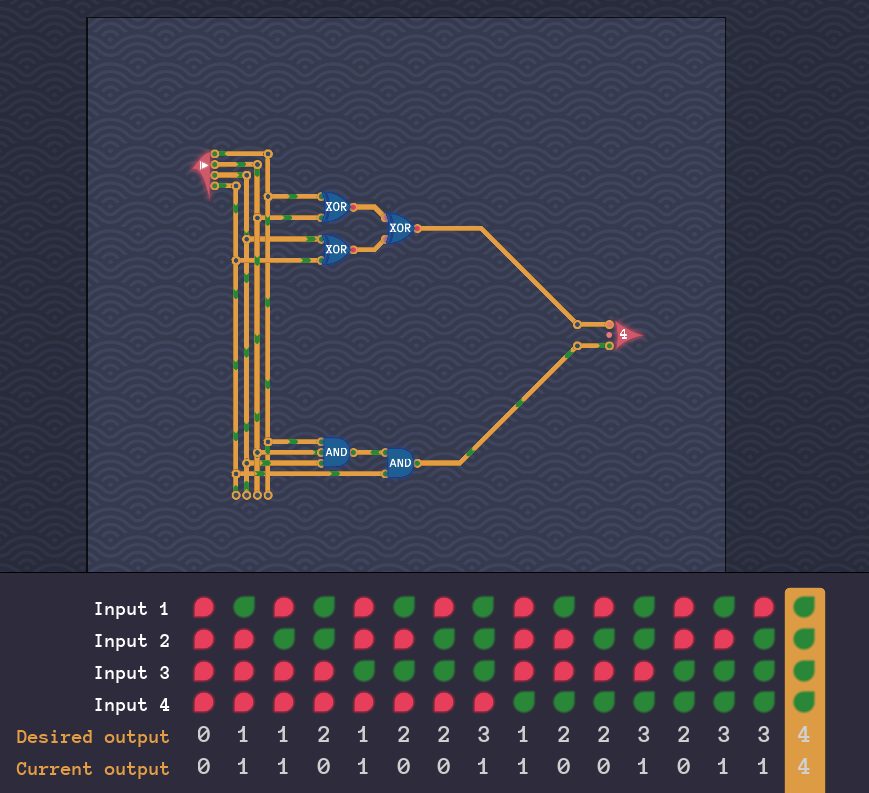
5：出力の2の位を生成する回路を設計する

入力のTの個数に注目して場合分けします。

入力のTの個数	2の位は？
0個	F（2の位まで到達しない）
1個	F（2の位まで到達しない）
2個	T
3個	T
4個	F

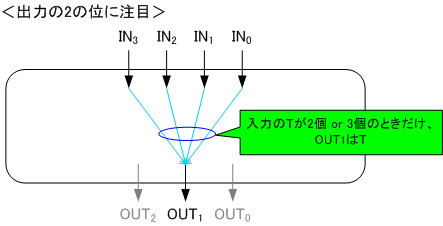
次に、「Tが2個の場合」と「Tが3個の場合」の具体的なパターンを見ていきます。

Tの個数	パターンの総数	具体的なパターン
2個	4C2=6通り	IN=1100b, 1010b, 1001b, 0110b, 0101b, 0011b
3個	4C3=4通り	IN=1110b, 1101b, 1011b, 0111b

上記の計10パターンのときのみに、2の位（OUT2）がT（1）になればよいのです。

(a)IN=1010b, 1001b, 0110b, 0101bについては、「2つのXOR＋AND」で判定できる。

(b)IN＝1100b, 0011bについては、「2つのAND＋XOR」で判定できる。

(c)IN=1110b, 1101b, 1011b, 0111bついては、「2つのAND＋XOR」で判定できる。

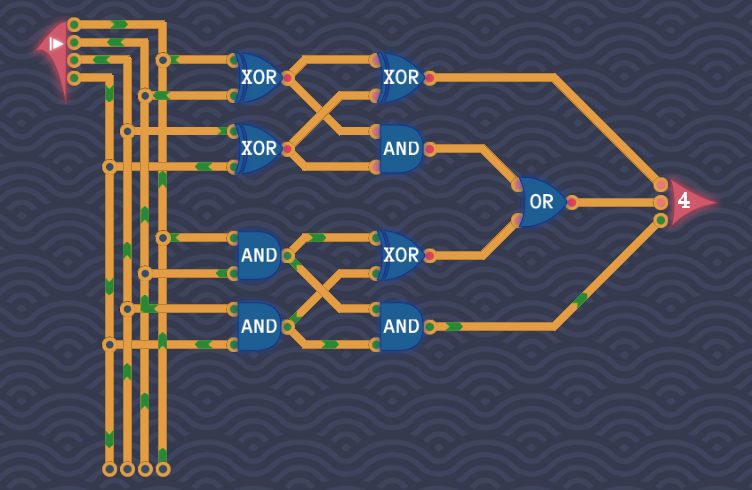
まとめると、INPUTを「2つのXOR＋AND」につなげる経路と「2つのAND＋XOR」につなげる経路を作り、それぞれの経路の出力をORに通します。

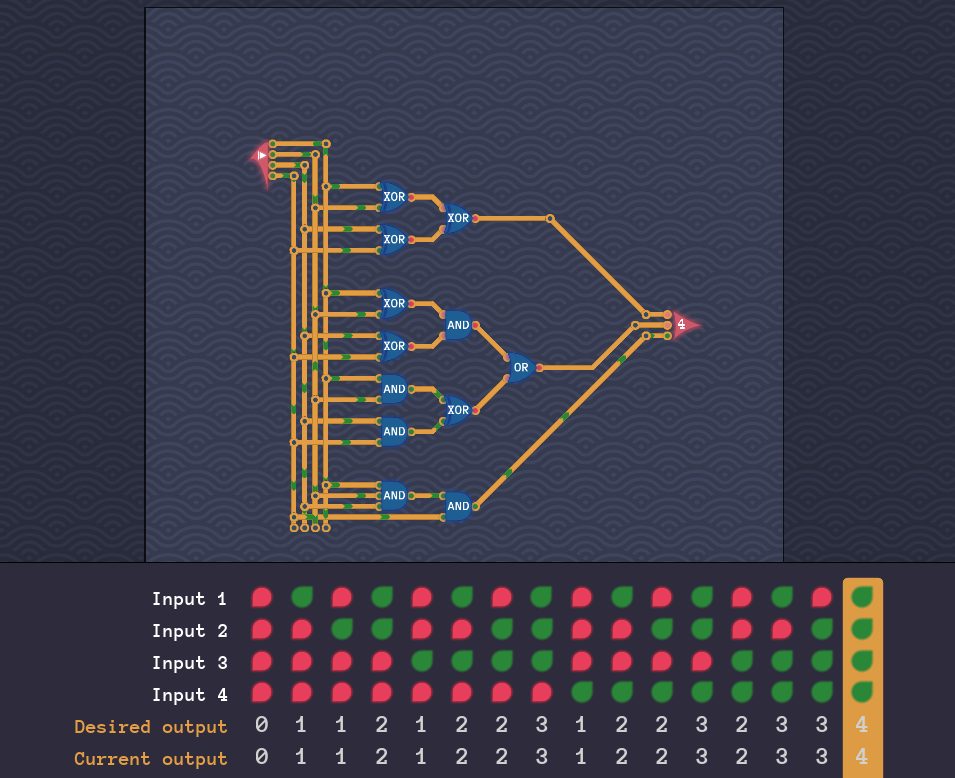
若干の変形バージョン【別解】