Unpack floating-point value【NandGame編】

2023年12月11日2024年6月18日

浮動小数点に関するレベルが開始

上級科目として、ここからは浮動小数点（floating point）演算を構築します。

浮動小数点は整数に比べて、より広い範囲の数を表現できます。

NandGameの浮動小数点

NandGameでは16ビットで浮動小数点値を表現します。

NandGameの浮動小数点記法は次のとおりです。

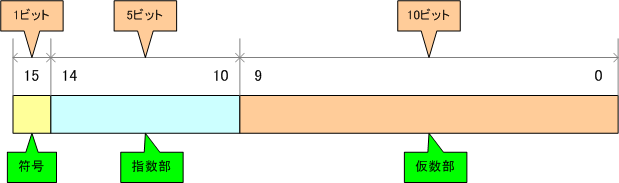
要素	ビット位置	ビット数	概要
sign	15ビット目 ※右が0ビット目とする。	1ビット	符号 ・0＝正、1＝負
exponent	10～14ビット目	5ビット	指数 ただし、バイアス指数なのでパック時には15を足す（詳細は後述）。
significand	0～9ビット目	10ビット	仮数かすう（シグニファンド） 有効数字を示す。 ただし、正規化された状態なので、アンパックする際には、「暗黙の最初の1」（後述）が存在することを忘れないように。

上記はNandGameにおける小数の表現ですが、実際のところ他の表現法もあります。詳細は次の記事を参考にしてください。

正規化

同一の数について複数の表現ができます。これでは比較や演算の際に不都合であるため、正規化という手続きを踏んで、標準的な形式に表現します。

例えば、10進数の228を浮動小数点数で表してみます。

まずは2進数に変換すると、228₁₀=1110 0100₂＝1110 0100₂×2⁰＝1.11001₂×2⁷になります。

実のところ、仮数の最初（一番左）のビットは常に1になるため、格納する必要ありません。これを暗黙の最初の1と呼びます。

暗黙の最初の1を無視すると、次のように表現できます。

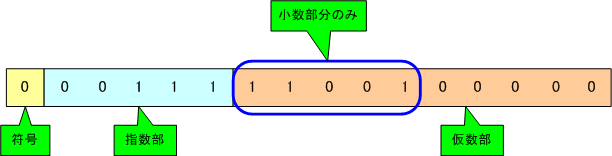
仮数部に小数部分のみを記述されています。これにより、1ビットを削減できます。つまり、表現できる数の範囲が広くなるわけです。

指数のバイアス（bias）

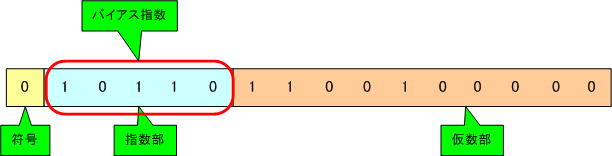
負の数を扱うのは不便なので、便宜上保存されている指数に15を加えます。加算された結果の指数をバイアス（下駄履き）指数といいます。

先の例にバイアス指数を適用すると、次のようになります。指数部が1 0110₂（＝7₁₀＋15₁₀＝22₁₀）になります。

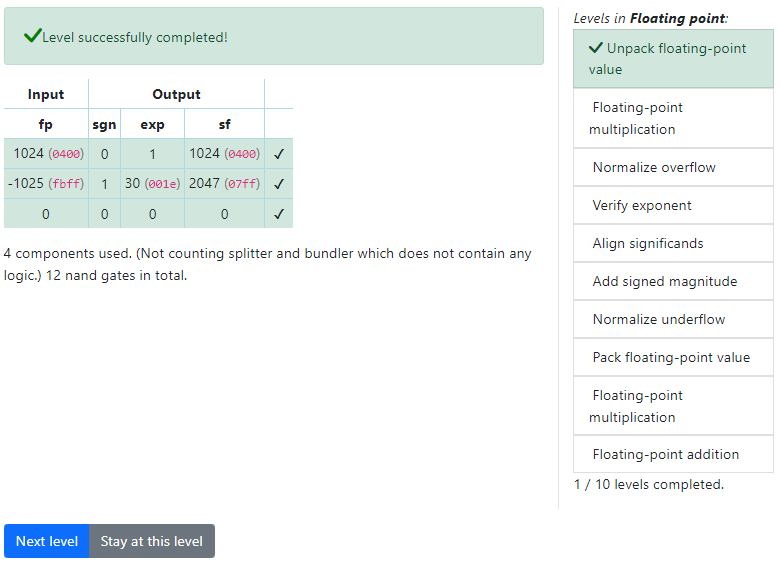
Unpack floating-point valueレベル

Unpack floating-point valueレベルのゴールは、正規化された浮動小数点数を3つの要素に分解する回路を実装することです。

回路の入出力は次のとおりです。

入力	・fp･･･正規化された浮動小数点数。16ビット。
出力	・sgn･･･符号。1ビット。 ・exp･･･指数。16ビット。 ※実際には16ビットも必要なく5ビットしか使いませんが、NandGameの仕様上入出力のデータ幅は1ビットか16ビットしか選べないのでこうなっています。 ・sf･･･仮数。16ビット。正規化を考慮して、暗黙の最初の1を付与する。

16ビット表現から33ビット（＝1＋16＋16）表現に変換することを「パックする」、その逆を「アンパックする」と呼ぶことにします。そして、16ビット表現の場合パックされた浮動小数点、33ビット表現の場合パックされていない浮動小数点と呼びます。

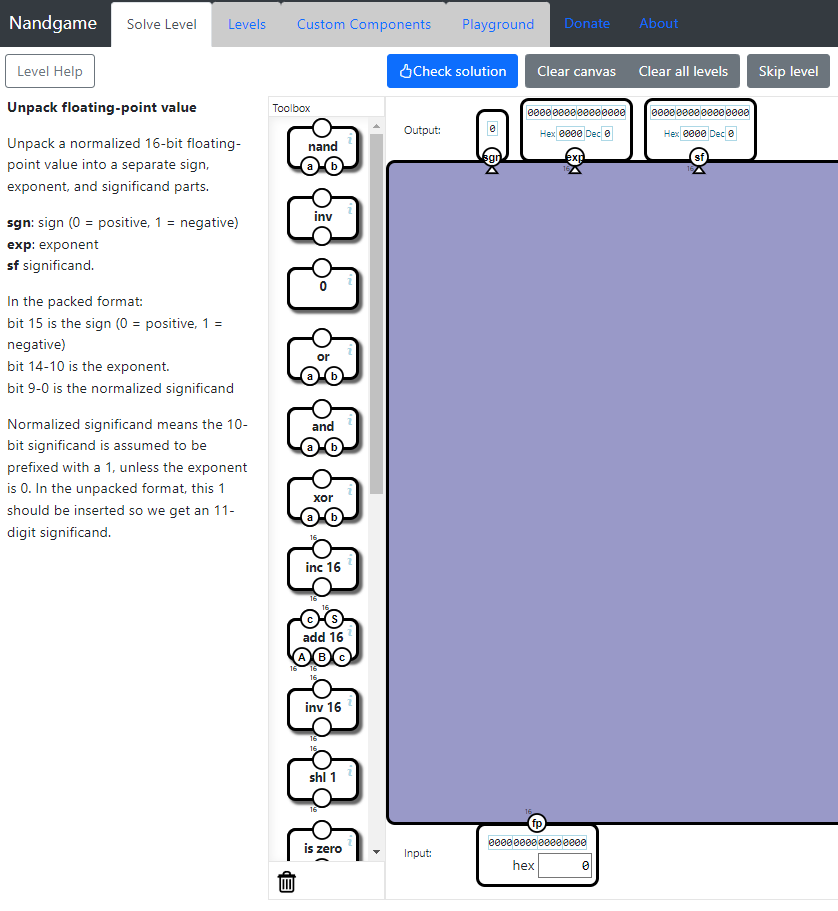
Unpack floating-point valueレベルを解く

1：指数部を取り出す

これは簡単です。「入力のfpの15ビット目」を出力sgrと直結するだけです。

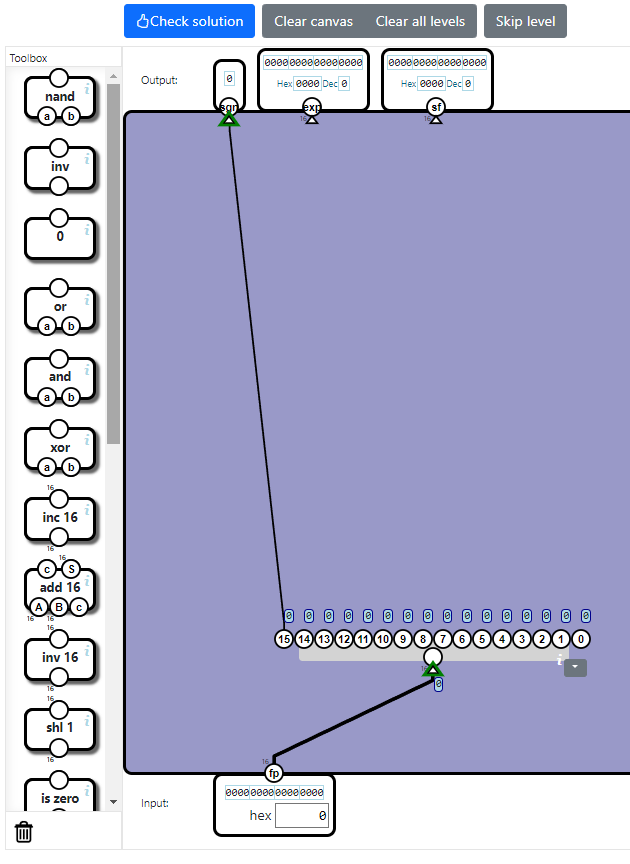
2：指数を取り出す

出力のexpからバイアス指数を出力します。そのためには、「入力のfpの10～14ビット目」を抽出してから、16ビット化するだけです。

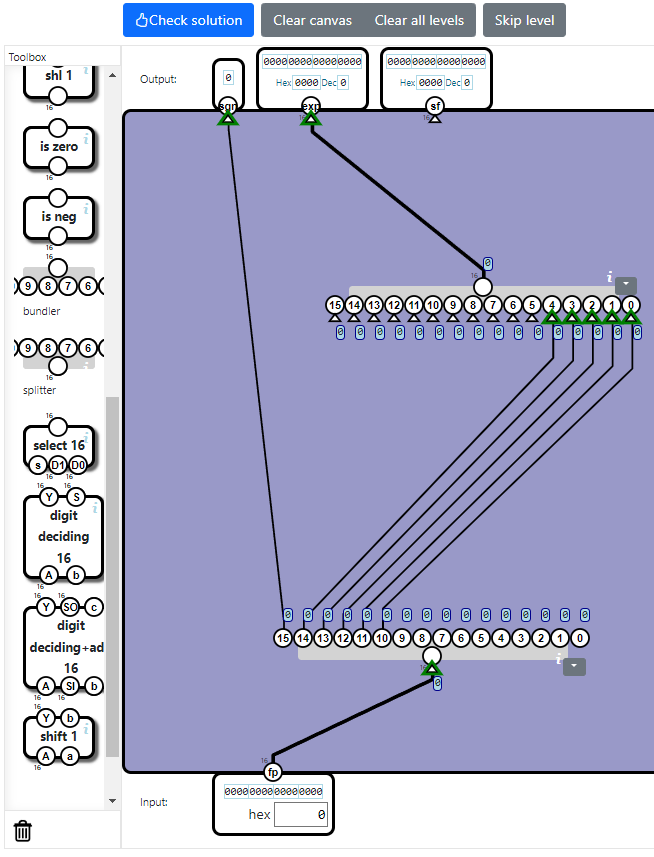
3：仮数を取り出す

まずは0～9ビット目を単純に取り出して16ビット化します。

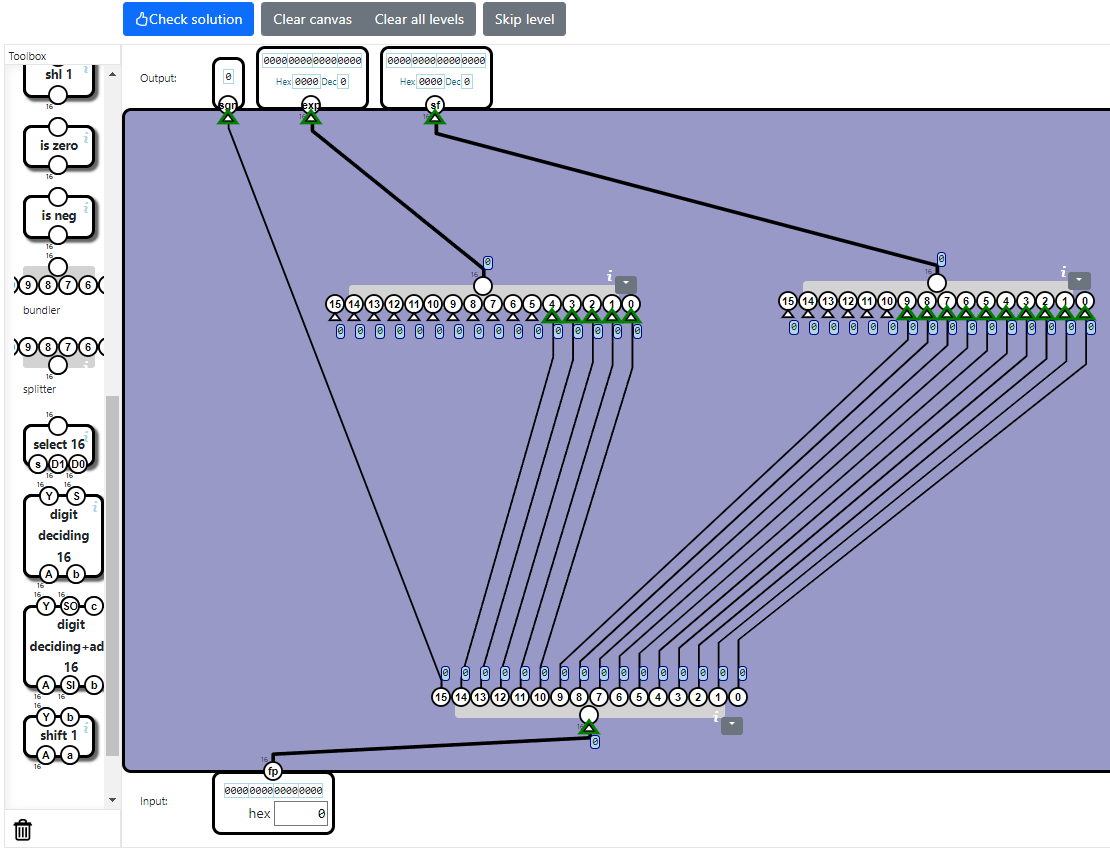
次に正規化について考えなければなりません。

指数が0以外、すなわち5ビットのうちどこかに1があるなら、暗黙の最初の1を付与するようにします。5入力のORゲートがあればそれ1つだけで済みますが、通常の2入力のORゲート（orコンポーネント）しか用意されていません。そこで、orコンポーネントと繰り返して使うことにします。

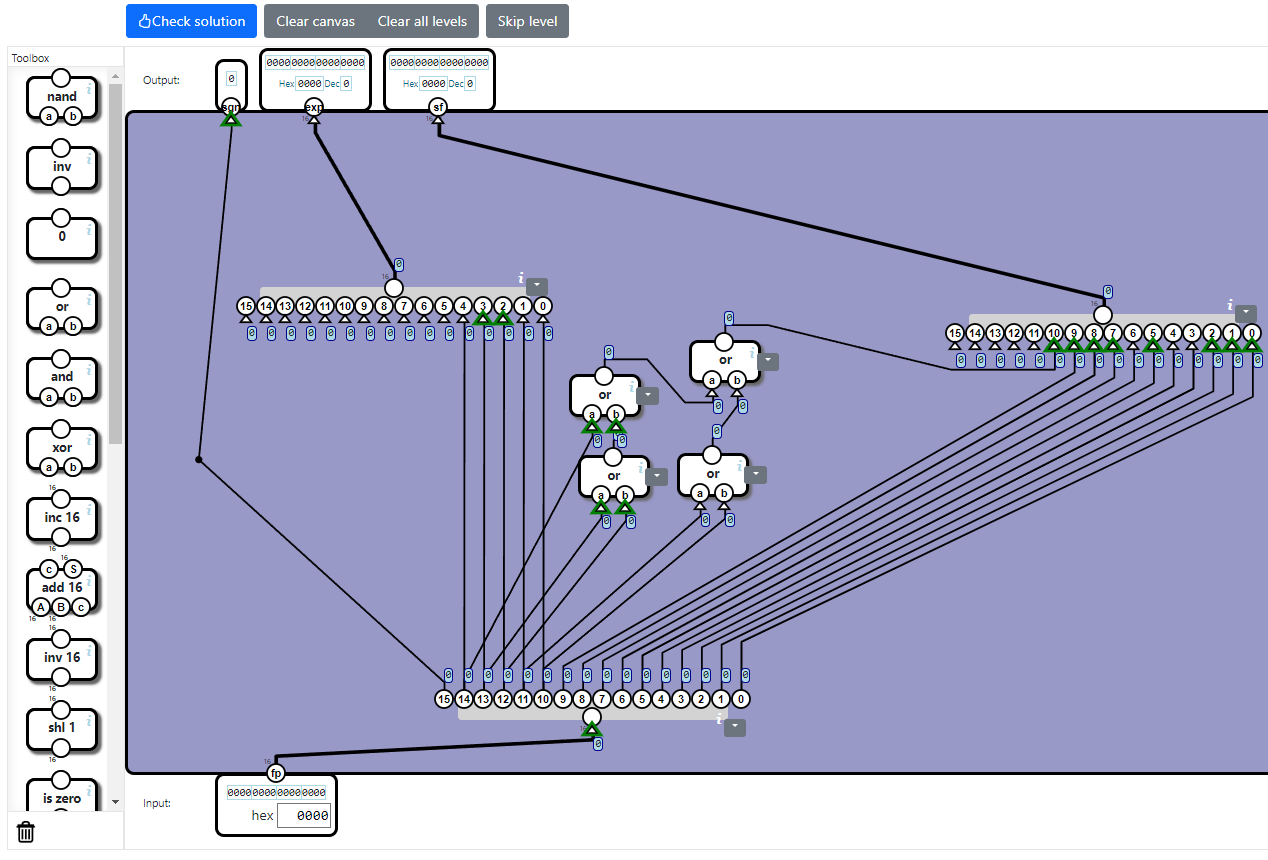
4：テストする

入力のfpに0400hや07ffhを指定して、挙動を確認してみましょう。

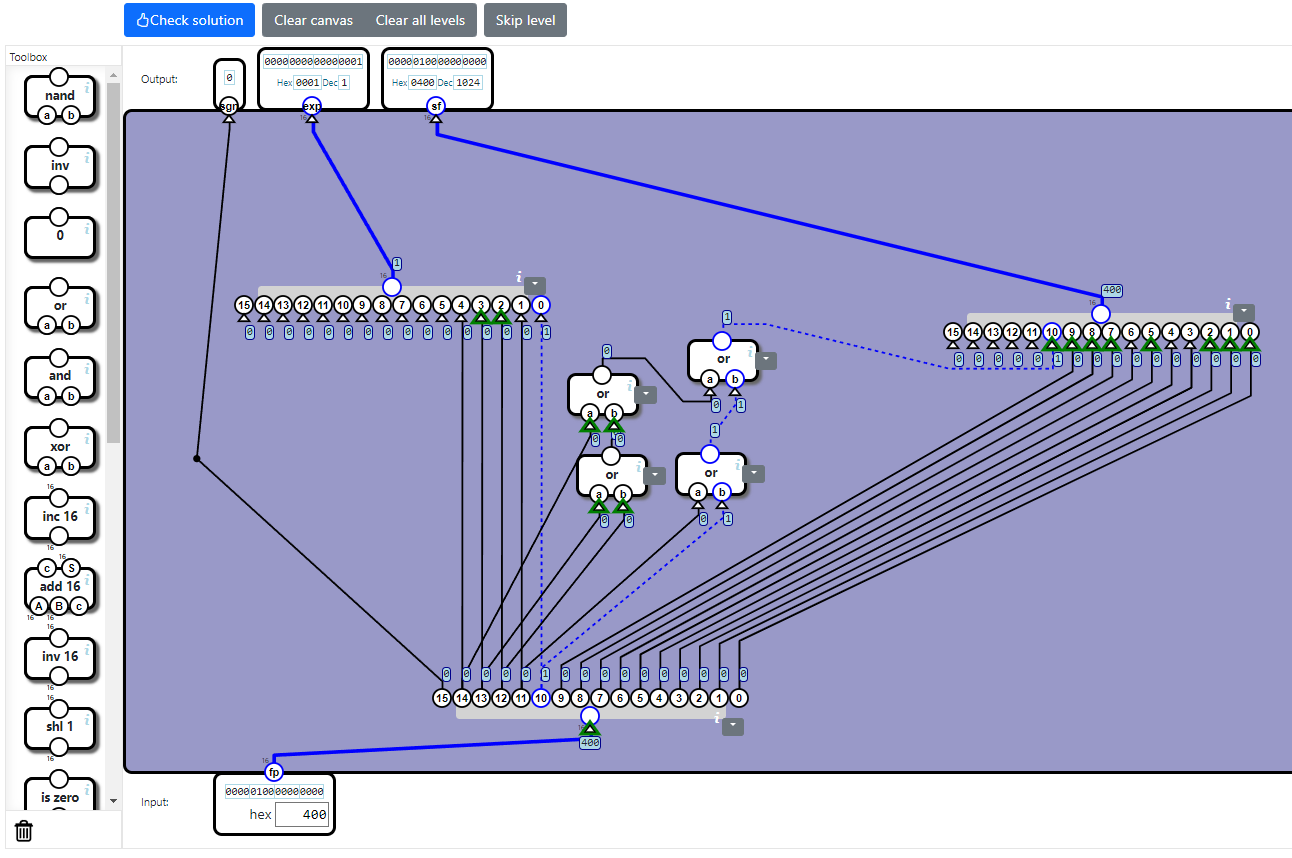
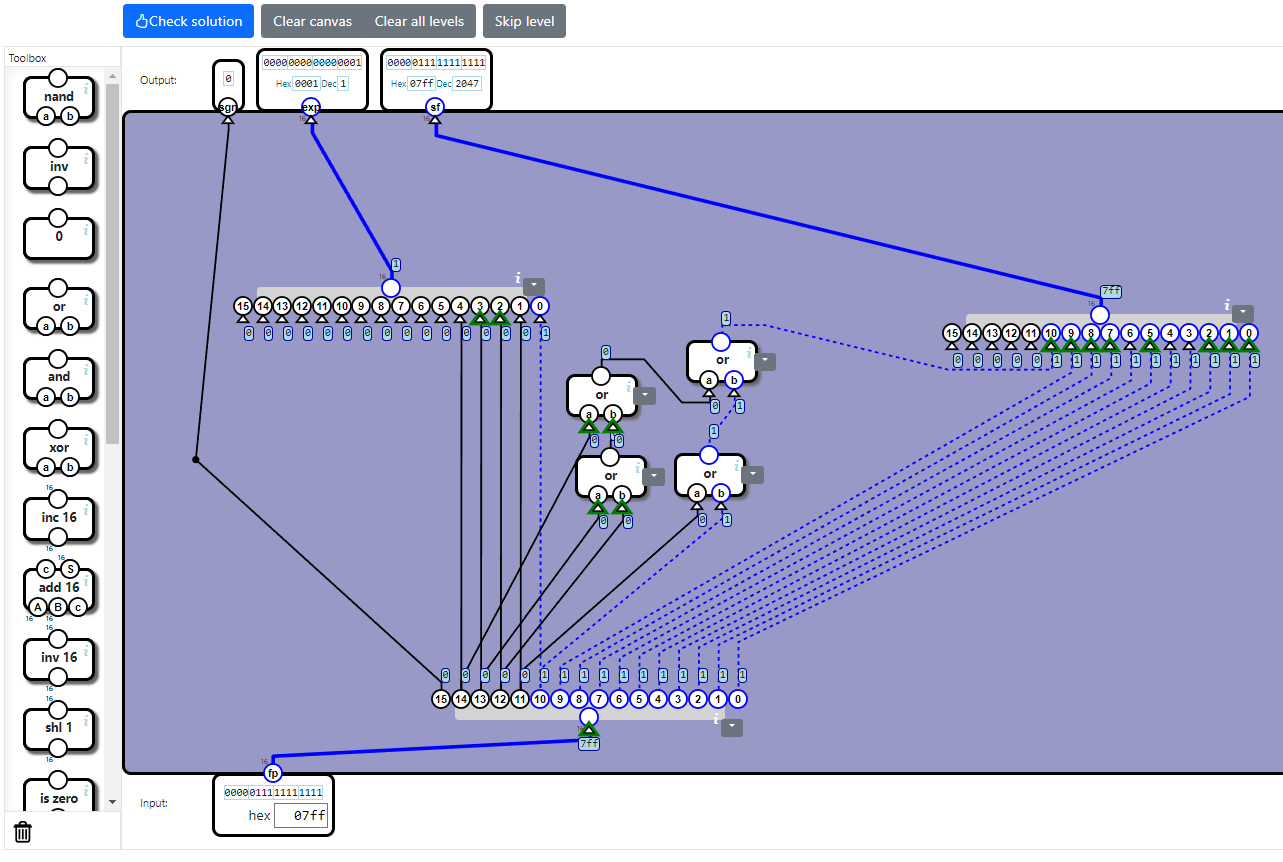
テストにパスするとクリアになります。