Equality【Turing Complete編】

2023年9月11日

Equalityステージ

Equalityステージのゴールは、1バイト（8ビット）版の一致回路を組むことです。

入力	・上のInput端子･･･1バイト。 ・下のInput端子･･･1バイト。
出力	・Output端子･･･1ビット。ONなら一致、OFFなら不一致。

Equalityステージを解く

1：回路の設計を検討する

XOR Gateステージにて、XOR回路は不一致回路と説明しました。

8ビット用のXORゲートがアンロックされていたら簡単ですが、このステージではまだ使えません。

そこで、2つのバイト入力を桁ごとに考えます。各桁をXORゲートに通します。その結果、ONなら不一致であったことを意味します。

1桁でも不一致なら、8桁全体で考えても不一致です。そこでORゲートでONが1つでも存在しないかを確認します。

今回の回路は不一致回路ではなく一致回路なので、最後にNOTゲートを通して反転させます。

2：回路を実装する

具体的に回路を組むと次のようになります。

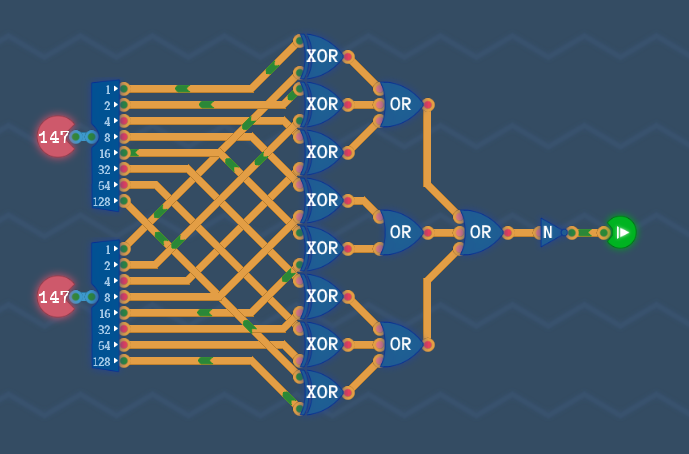
2：テストする

クリアすると、Equalコンポーネントがアンロックします。

「ビット列が一致するなら、片方をビット反転させてから加算すると必ず全ビット1になる」という事実を利用する【別解】

2つのビット列が一致するなら、片方をビット反転させてから加算すると必ず全ビット1になります。桁上がりも起きません。

この事実についてピンとこない場合は、具体的な数値で確認してみましょう。

[例1]A=B=0110 0110bのように、AとBが一致のケースを考えます。

A=0110 0110b、￣B=NOT(B)=1001 1001b

ADD(A, ￣B)=A+B＝0110 0110b+1001 1001b=1111 1111b＝0xFF

全ビットが1になっています。

[例2]A=0110 0110b、B=0100 0110bのように、AとBが不一致のケースを考えます。

A=0110 0110b、￣B=NOT(B)=1011 1001b

ADD(A, ￣B)=A+B＝0110 0110b+1011 1001b=1 0001 1111b

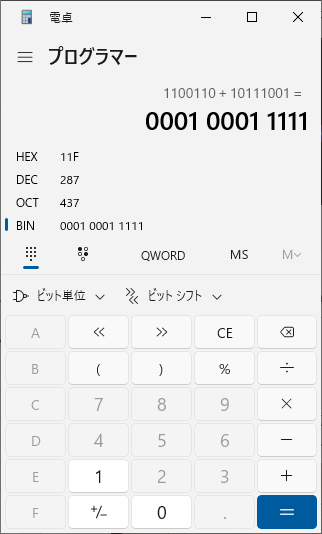
全ビットが1になっていません。今回のケースでは桁が上がりが起こっています。ただし、桁上がりが起こるかどうかは、扱うビット数に依存します。

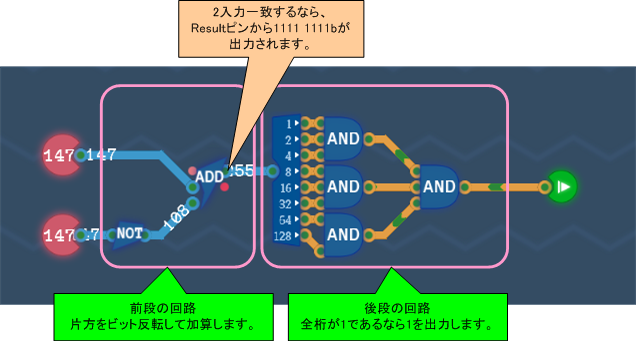
以上の事実を踏まえて、回路を実装すると次のようになります。

・前段の処理･･･ADD（A, ￣B）を計算する。8 Bit NOTコンポーネント、Addコンポーネントを利用。

・後段の処理･･･全ビットが1であることを判定する。1バイトの各桁についてANDゲートを通して結果を得ればよい。1つでも0があったらANDゲートの最終結果は0になるため。

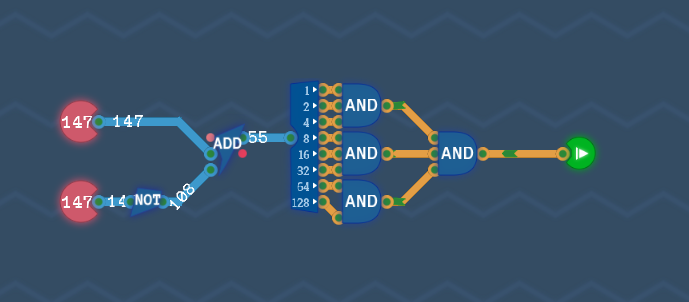
以上を踏まえて回路を組むと、次のようになります。

「ビット列が一致するなら、片方を符号反転させてから加算すると必ず0になる」という事実を利用する【別解2】

2つのビット列が一致するなら、片方を符号反転させてから加算すると必ず0になります。0にならなければ、最初の2つのビット列が一致していません。

符号反転については、Signed Negatorステージで解説しました。このステージをクリアしたことで、符号判定を実現するNegateコンポーネントをアンロックしています。

AddコンポーネントのResultピンから出てくるのは1バイトになります。一致するときに0が出てきますが、これは1バイト幅の0、すなわち0000 0000bです。

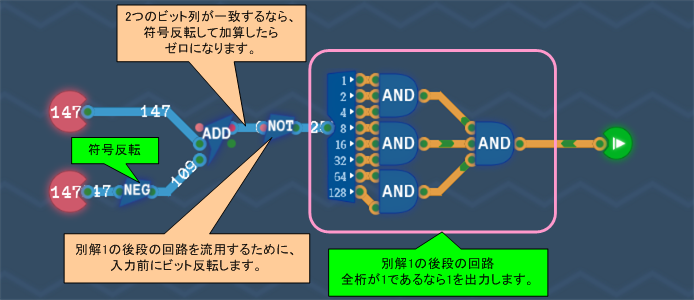
別解1の後段の入力とは逆のパターンになっています。別解1の後段を再利用するには、入力を8 Bit NOTコンポーネントで反転させてしまえばよいのです。

以上を踏まえて回路を組むと、次のようになります。

XNOR回路は一致回路であることを利用する【別解3】

XOR回路は不一致回路でしたが、対してXNOR回路（XOR＋NOTを意味する）は一致回路になります。

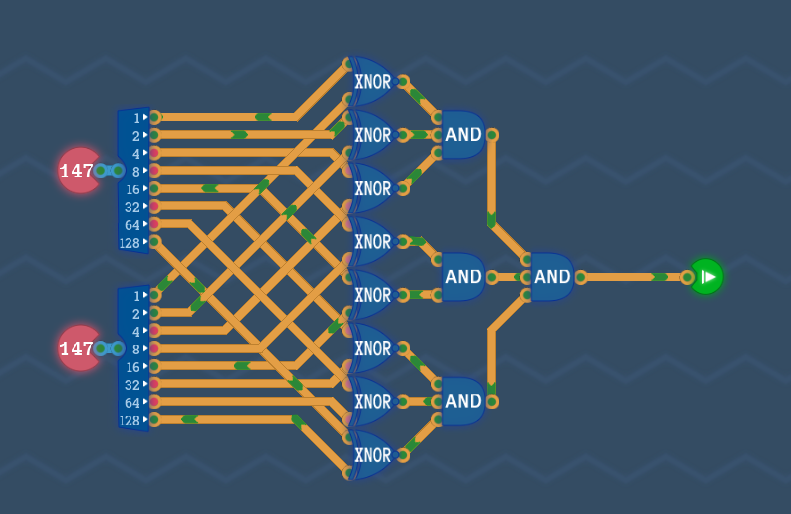
XNORコンポーネントの入力が一致すれば、出力は1になります。全桁についてXNORコンポーネントを通した結果、すべてが1であれば、最初の入力データは桁数にかかわらず一致しているはずです。すべてが1であることのチェックには多入力型のANDコンポーネントが使えます。8入力型のものはないので、2入力型と3入力型を多段することで代用できます。

以上を踏まえて回路を組むと、次のようになります。

好みの問題かもしれませんが、最初の解答と比べるとこちらの方が自然な回路といえます。

なぜなら、本ステージではバイトデータ用の一致回路を組むことが目的あり、その内部も一致回路で構成したほうが自然な発想だからです。