Floating-point multiplication【NandGame編】
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
浮動小数点数の乗算
浮動小数点の演算では、加算や減算より乗算の方が簡単です。そこで、乗算の解説から始めます。
浮動小数点の乗算は「仮数の乗算」と「指数の加算」で実現されます。
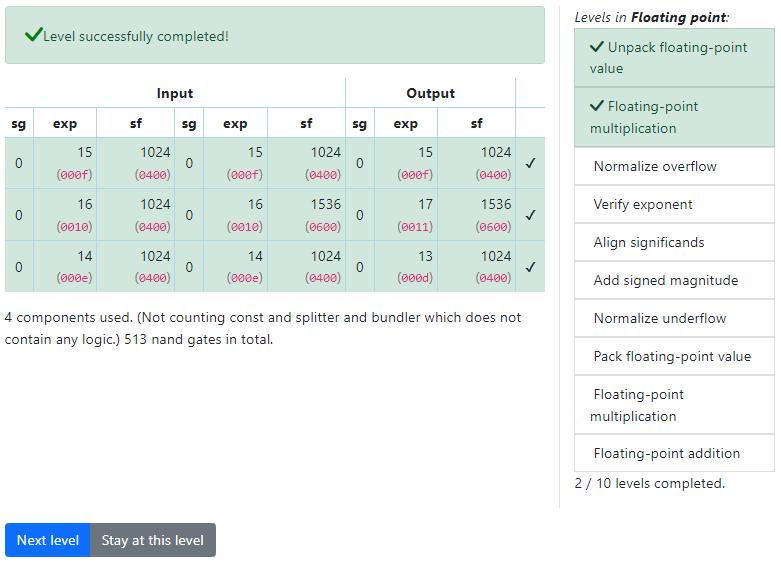
Floating-point multiplicationレベル
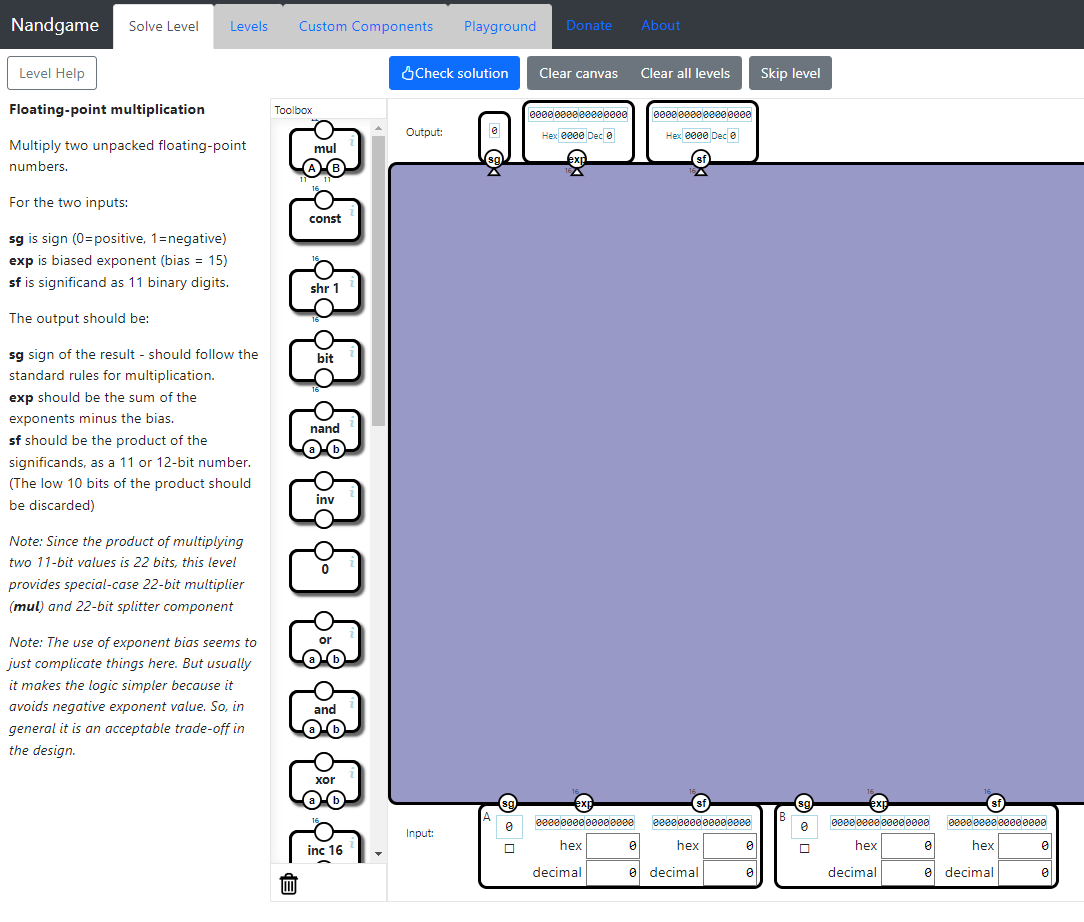
Floating-point multiplicationレベルのゴールは、浮動小数点の乗算を実現する回路を組むことです。
回路の入出力は次のとおりです。
| 入力 | A | パックされていない浮動小数点数。33ビット(=1+16+16=sg分+exp分+sf分) ・sg:符号。0=正、1=負。 ・exp:バイアス指数 ・sf:仮数 |
| 入力 | B | パックされていない浮動小数点数。33ビット。 |
| 出力 | 乗算結果の(パックされていない)浮動小数点数。 ・sg:「Aのsg」と「Bのsg」の乗算結果。 ・exp:「Aのexp」と「Bのexp」を加算し、その計算結果からバイアス分を引いたもの。 ※AとBの両方がバイアス化されているため。加算するとバイアス1回分余分になる。 ・sf:「Aのsf」と「Bのsf」を乗算し、その計算結果を補正したもの。 11ビット値を乗算すると、21ビットまたは22ビットが得られる。 出力値である浮動小数点の仮数は11ビットまたは12ビットにするため、乗算結果の下位10ビットを切り捨てる。 |

余談ですが、仮数の計算に切り捨て処理があるため、浮動小数点演算によって精度を失われる可能性があります。
Floating-point multiplicationレベルを解く
1:出力のsgを計算する回路を組む
sgは符号であり、「正=0」「負=1」と定義されています。
符号の乗算表は次のとおりです。
| Aのsg | Bのsg | 出力のsg |
|---|---|---|
| 正 | 正 | 正 |
| 正 | 負 | 負 |
| 負 | 正 | 負 |
| 負 | 負 | 正 |
このままではわかりにくいので、「正=0」「負=1」で置き換えます。
| Aのsg | Bのsg | 出力のsg |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
これはXORゲートの真理値表そのものです。つまり、xorコンポーネントを1つ通すだけで、出力のsgにつなげるだけです。
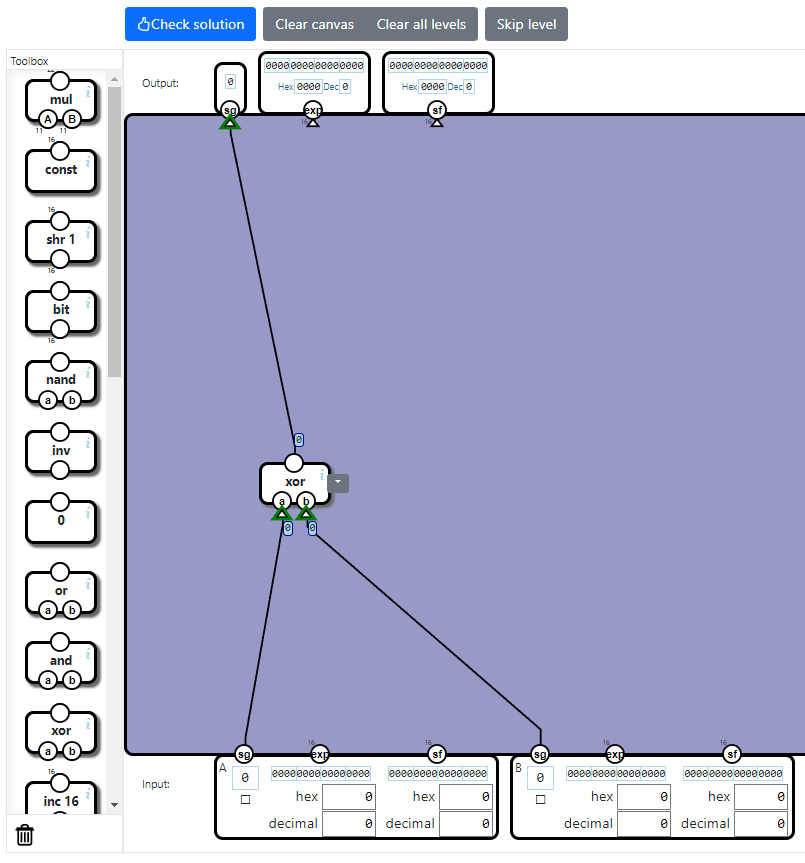
2:出力のexpを計算する回路を組む
出力のexpについては、入力のexp同士を加算し、バイアス分の15を引けばよいだけです。
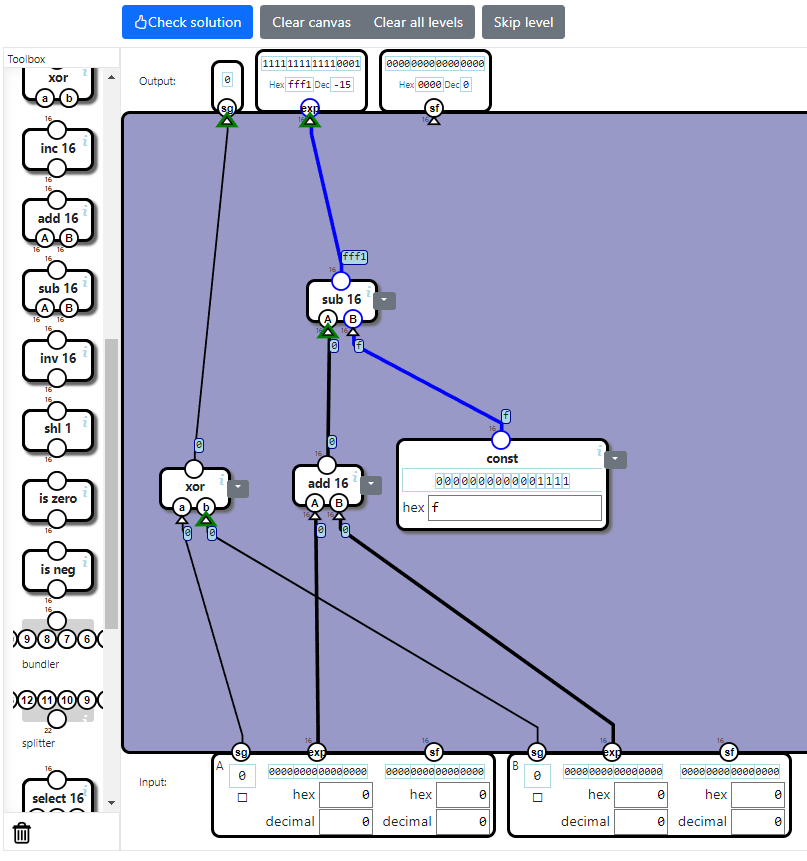
3:出力のsfを計算する回路を組む
当該レベルのために、mulコンポーネントと22ビット用のsplitterコンポーネントが用意されてます。
mulコンポーネントは、2つの11ビット値の乗算の積を実現する、22ビット乗算器です。出力ピンの脇に小さく「22」とあることから、22ビット値を出力することがわかります。
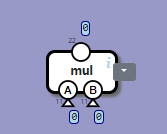
22ビット用のsplitterコンポーネントは、22ビット値を各桁に分離する回路です。
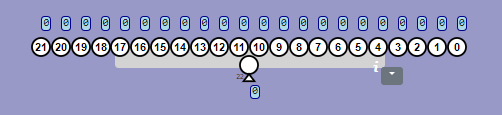
これらのコンポーネントを活用すると、次の回路になります。
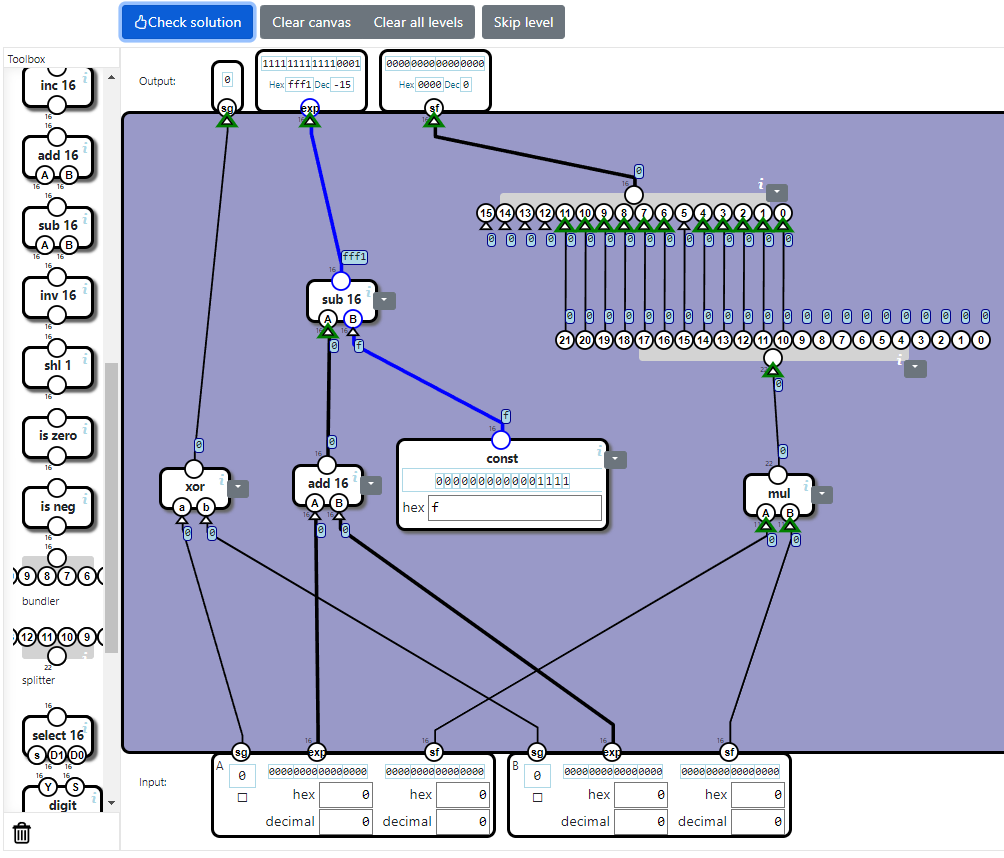
4:テストする
テストにパスすると、クリアになります。