MOSFETで論理回路を実現する
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
MOSFETを活用すれば論理回路を作れる
NチャネルとPチャネルのMOSFETはゲートに電圧がかかっているかで、スイッチングを実現できます。
お互い逆の動作をするので、うまく組み合わせると論理演算を実現する回路、論理回路すなわちを実装できます。
MOSFETでAND回路を組む
| A | B | Z |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
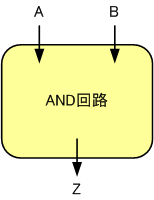
1:AND回路の入出力に着目する
入力はAとB、出力はZです。まだAND回路の中身はブラックボックスで構いません。
2:単純なワイヤリングを考察する
まず単純に入出力を直接電線でつないでみます。
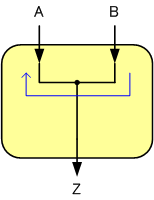
真理値表における「A=B=0」「A=B=1」のときを満たしています。
しかし、「A=0、B=1」のとき、青い矢印のように電流がAに逆流してしまいます。
※AとBにダイオードを挟めば逆流を防止できます。
以降では、真理値表の残りの2パターンを満たす回路を考えてみます。
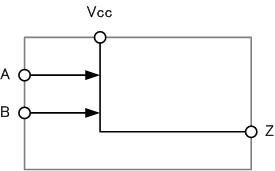
3:スイッチを利用した回路にする
AとBをスイッチを制御することと見なせば、次の回路のように直列化すればよさそうです。
これでAND演算の真理値表は満たします。
4:MOSFETでスイッチを実現する
ここではスイッチをMOSFETで実現するものとします。
入力が1のときに電流を流せるようにするには、NチャネルMOSFETを用います。
NチャネルMOSFETはゲートが1なら電流を流し、0なら流しません。
これで置き換えると次のようになります。
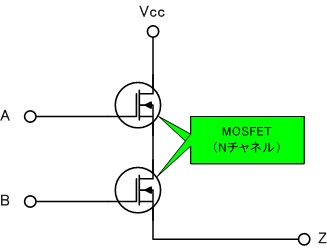
しかし、まだリアルな回路としては不完全です。
A=0か、B=0なら、VccとZは切断された状態です。つまり、Zには何も接続されておらず、安定した信号を出力できません。
そこで、この状態のとき確実にZ=0にするために、次のように回路を追加します。

5:各パターンを確認する
[1]A=B=0の場合
ONは導通、OFFは遮断になります。
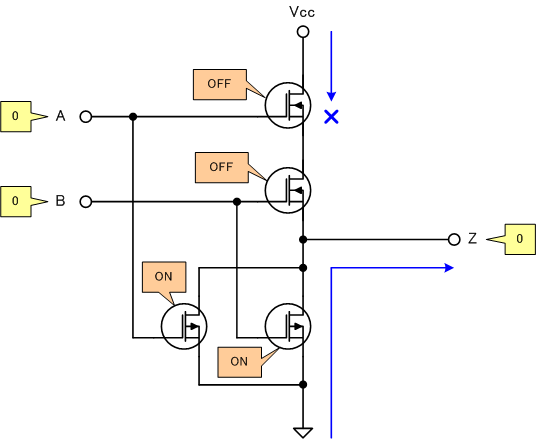
[2]A=0、B=1の場合
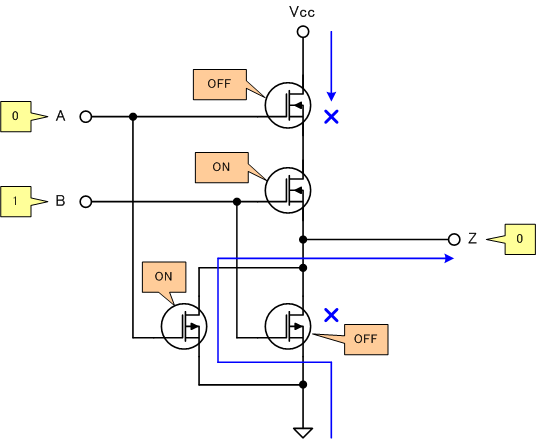
[3]A=1、B=0の場合
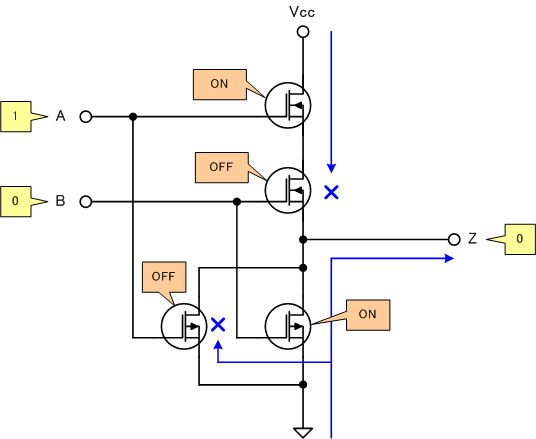
[4]A=B=1の場合
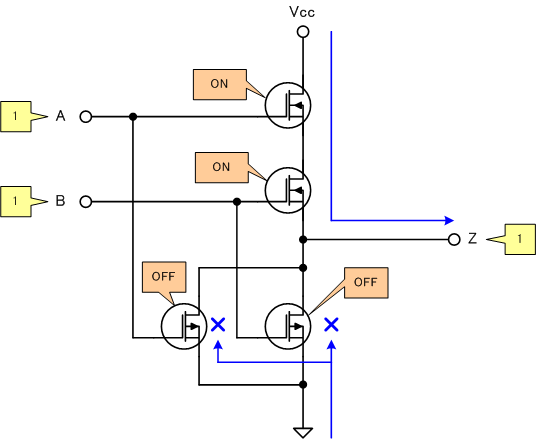
ゆえに、MOSFETでAND回路を組み立てできました。
MOSFETでOR回路を組む
| A | B | Z |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
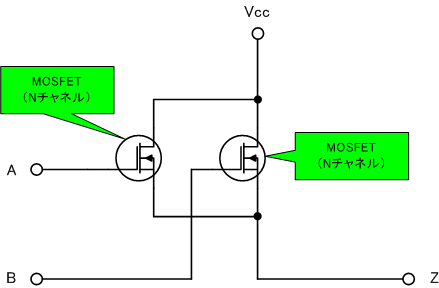
A=B=0のときに、Zが接続されてない状態になり、不安定になります。
これを解決するために、次のように回路を追加します。
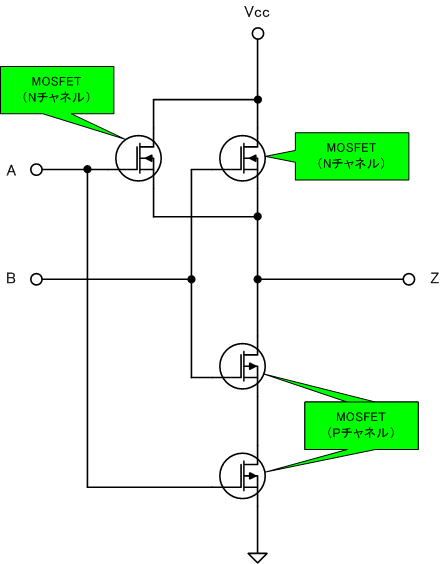
AND回路の逆さまになっています。
[1]A=B=0の場合
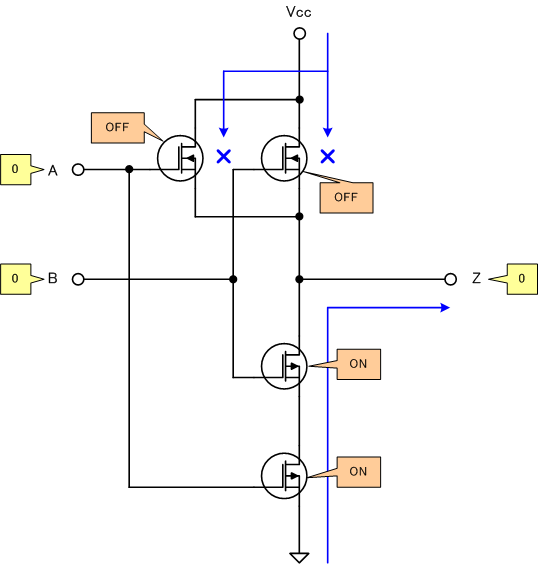
[4]A=0、B=1の場合
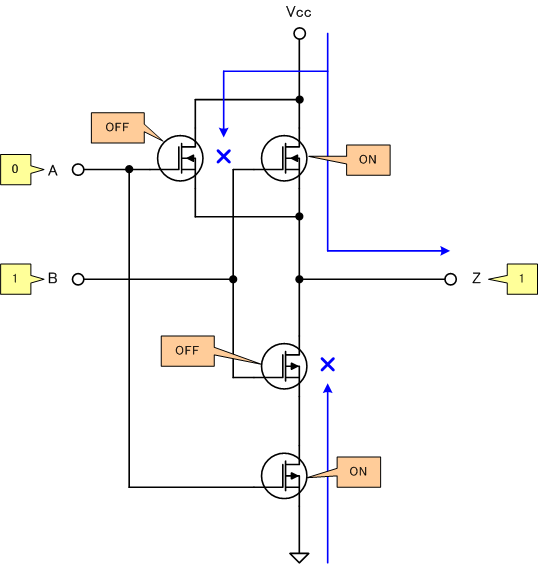
[3]A=1、B=0の場合
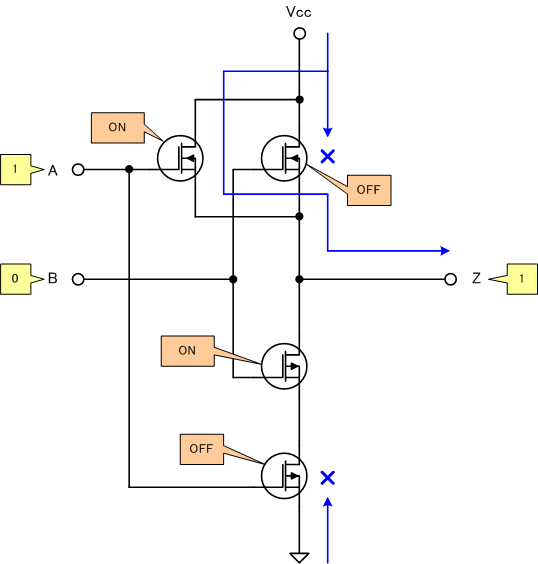
[4]A=B=1の場合
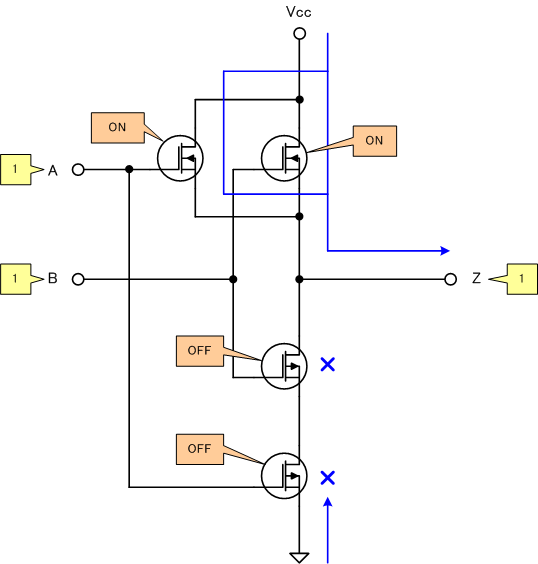
MOSFETでNOT回路を組む
| A | Z |
|---|---|
| 0 | 1 |
| 1 | 0 |
MOSFETによるAND回路において、A=Bをつないでしまいます。
するとNOT演算を実現できます。
ただし、同じ回路が並列に組み込まれているわけで、部品的には無駄が多いので、次のように最適化できます。
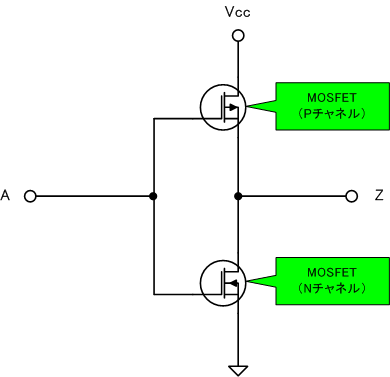
AND回路やOR回路よりシンプルなので、このNOT回路(インバーター)が基本回路と捉えることができます。
[1]A=0の場合
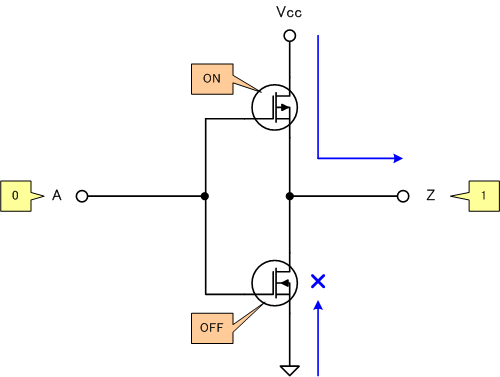
[2]A=1の場合
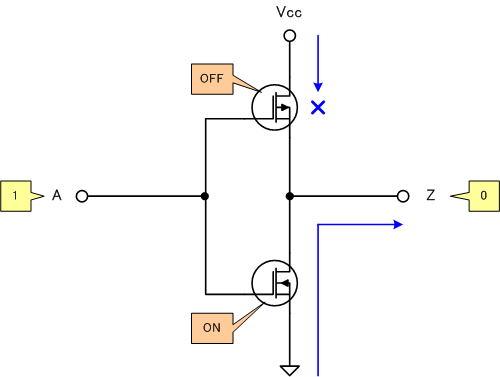
おわりに
Turing Completeでは、NANDからスタートして論理演算を実現しました。
当該ページでは、MOSFETでAND・OR・NOT演算を実現できました。
後は組み合わせれば、別の論理回路を組めます。
参考文献
P28-39
P51-58