Page09 NVMERO SANCTVM【Alchemia編】
はじめに
いつもブログをご覧いただきありがとうございます。
ミジンコに転生したIPUSIRONです😀
ページの内容
上段には異なる文字体系のメッセージが並んでいます。
下段には6行のメッセージ（詩文）があります。
その下のフッターには"NVMERO SANCTVM"（ラテン語で「聖なる数」）、木星のシンボルがあります。
木星のシンボルは、錬金術で錫（スズ）を表します。
攻略への道
解読1
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
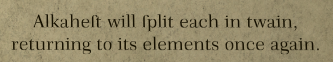
1-2行目のメッセージをlong sで書き起こすと、以下のようになります。
Alkaheft will fplit each in twain,
returning to its elements once again.
このままでは読みにくいので、現代英語（short s）に変換します。
Alkahest will split each in twain,
returning to its elements once again.
以下がその和訳になります。
アルカヘストがそれぞれを二つに分け、
再びその元素へと還す。
“twain"は古英語で「2つ」を意味します。"twin"と同語源です。
“Alkahest"だけでGoogle検索するとノイズが多いので、"Alkahest"+"Alchemy"で検索します。
すると、錬金術の世界に"Alkahest"という用語があることがわかります。
https://en.wikipedia.org/wiki/AlkahestAlkahest（アルカヘスト）は、錬金術における万能溶剤のことです。16世紀の錬金術師パラケルススが提唱しました。
あらゆる物質を溶かし、元の構成要素に分解できるとされた伝説の物質とされます。
https://en.wikipedia.org/wiki/Paracelsusところで、2行目に登場する単語"elements"は、「元素」の他に「構成要素」という意味合いもあります。
よって、メッセージは「Alkahestで2つに分割し、構成要素にする」ということを意味します。
ここで、上段の謎のメッセージを見てください。
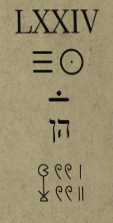
1行目の"LXXIV"がローマ数字であることに気づくかもしれません。
| 記号 | 値 |
|---|---|
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
L + X + X + IV
↓ ↓ ↓ ↓
50 + 10 + 10 + 4 = 74
つまり、1行目は数74になります。
メッセージの内容を考慮すると、「数を2つに分割するのでは？」と思いつきます。
数の分割といえば、素因数分解が代表的です。
74を素因数分解すると、「74＝2×37」になります。ちょうど2つに分割できたことから、メッセージの内容とも矛盾します。
以上のことから、上段の2行目以降も数字ではないかと想像できます。
別解1
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
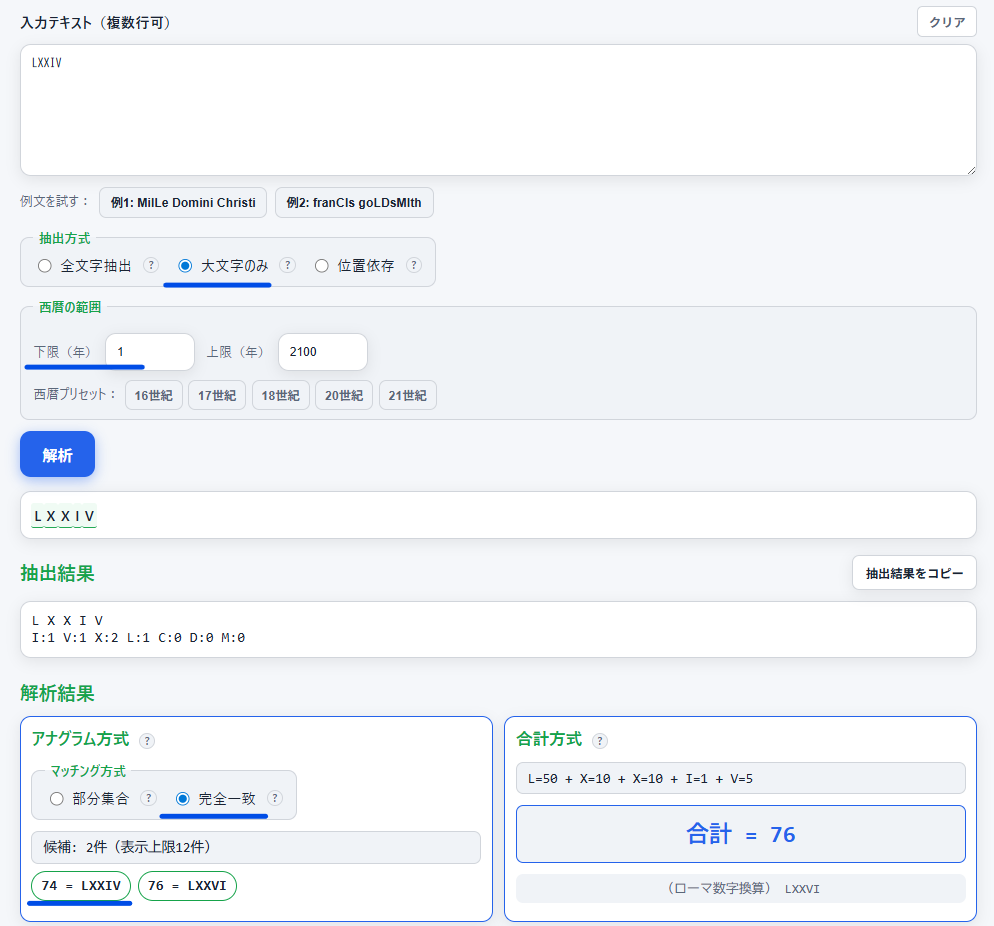
Epigraph Chronogrammerは本来クロノグラムを解読するためのツールですが、ローマ数字に変換するためにも活用できます。
https://ipusiron.github.io/epigraph-chronogrammer/「西暦の範囲」の下限を1にするのがポイントです。
※デフォルトでは1500になっています。そして、0は非対応です。
解読2
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
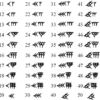
上段がすべて数を指しているという仮定の下、2行目の分析に進みます。
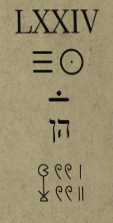
ローマ数字ときたら、ギリシャ数字（Greek number）がピンとくるかもしれません。しかし、シンボルがよく見かけるギリシャ文字ぽくないので、もう少し考察します。
ゲームAlchemiaが背景とするのは錬金術の時代なので、古代ギリシャ文字（Ancient Greek number）が採用されている可能性もあります。
1文字目は横三本線のシンボルです。ギリシャ文字の中で、この特徴を持つ文字はクシー「Ξ」（クシーの大文字、クシーの小文字は「ξ」）しかありません。
2文字目は円の中に点があるシンボル「⊙」です。ギリシャ文字のシータ「Θ」（シータの大文字、シータの小文字は「θ」）は、円の中に横線がある形で書かれることが多いですが、横線の代わりに点であることもあります。
ギリシャ数字には「アッティカ式」と「イオニア式」の2つの方式があります。アッティカ式は縦棒を使うため、ここではギリシャ文字をそのまま使うイオニア式で計算してみます。
https://ja.wikipedia.org/wiki/ギリシアの数字
https://en.wikipedia.org/wiki/Greek_numerals
上記の表を用いてギリシャ文字から数字に変換します。
「ΞΘ」⇒「ξθ」⇒「60+9」⇒69
数69が得られましたので、今度は素因数分解します。
69＝3×23
確かに2つの素数に分割できました。
解読3
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
上段がすべて数を指しているという仮定はかなり信憑性が高くなってきました。
それでは、3行目の分析に進みます。
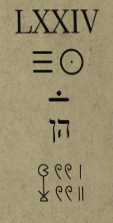
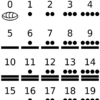
3行目の文字がどの文明のものかは消去法になります。
マヤ、エジプト、バビロニア、中国などが候補に挙がります。
その過程で、マヤ数字（Maya numerals）にそっくりな数字があることに気づきます。
https://en.wikipedia.org/wiki/Maya_numeralsマヤ数字は世界でもっともシンプルな記数法の1つであり、点と横線だけで0-19を表現できます。
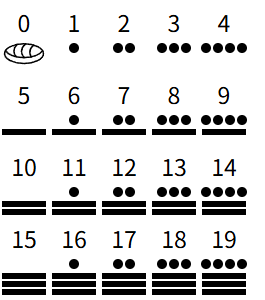
6に対応する文字が該当します。
6を素因数分解すると、6=2×3となります。
解読4
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
4行目に進みます。
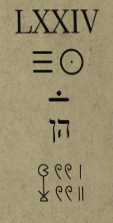
הנ
これは明らかにヘブライ文字の形状をしています。
ヘブライ語は右から左に読むことに注意してください。
https://ja.wikipedia.org/wiki/ヘブライ数字ヘブライ文字は以下のように数字と対応しています。
| 1の位 | 10の位 | 100の位 |
|---|---|---|
| א = 1 | י = 10 | ק = 100 |
| ב = 2 | כ = 20 | ר = 200 |
| ג = 3 | ל = 30 | ש = 300 |
| ד = 4 | מ = 40 | ת = 400 |
| ה = 5 | נ = 50 | |
| ו = 6 | ס = 60 | |
| ז = 7 | ע = 70 | |
| ח = 8 | פ = 80 | |
| ט = 9 | צ = 90 |
ヘブライ語には数字専用の記号がなかったため、文字で数を表したのです。
現在の学術的見解では、ギリシャのイソプセフィアとヘブライのゲマトリアは、ほぼ同時期（紀元前数世紀）に独立または相互影響で発展したと考えられています。
・紀元前8世紀頃：ギリシャ・ヘブライでアルファベット数字が使われ始める
・紀元前3世紀頃：イソプセフィア・ゲマトリアの実践が文献に登場
・紀元後：カバラでゲマトリアが神秘主義的に発展
1桁目が「ה」[1]文字「ヘー」（He）に該当します。、2桁目が「נ」[2]ぱっと見では識別できないかもしれませんが、文字「ヌン」（Nun）に該当します。です。
נ + ה = 50 + 5 = 55
Gematira CipherLabでもヘブライ数字を解読できます。
https://ipusiron.github.io/gematria-cipherlab/「ゲマトリア」タブを選び、テキスト入力欄に「הנ」を指定し、[計算]ボタンを押します。
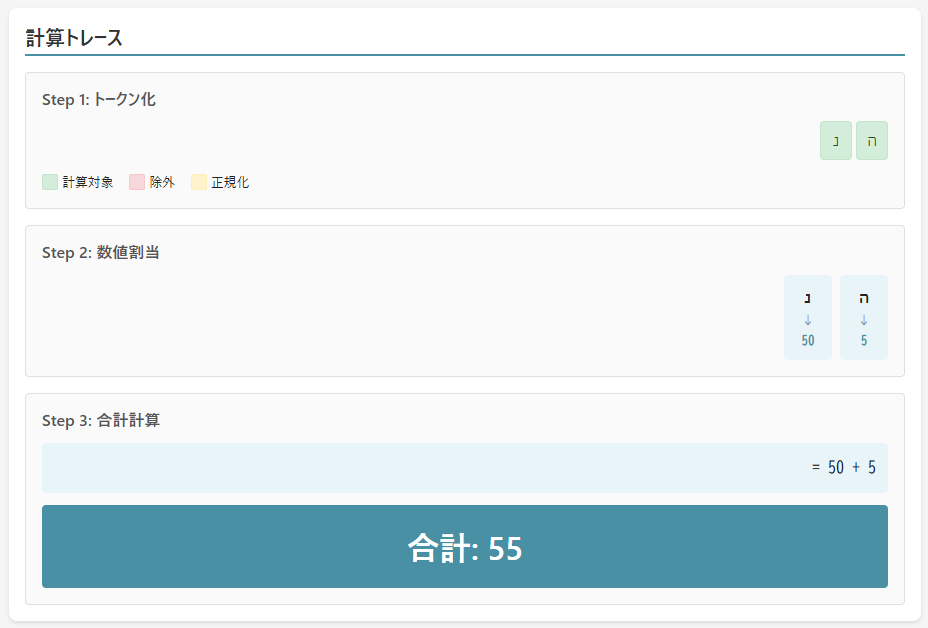
55を素因数分解すると、5×11になります。
解読5
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
最後の行に挑戦します。
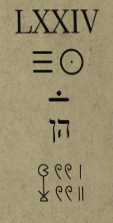
かなり特徴的な文字です。特に左側はパックマンなのか花なのか不思議な文字であり、象形文字ではないかと推測できます。
象形文字の代表としてはヒエログリフ（古代エジプト文字）が挙げられます。
ヒエログリフ数字は10進法で、各桁に専用の記号があります。
| 記号 | 名称 | 値 |
|---|---|---|
| | | 棒（ストローク） | 1 |
| ∩ | かかとの骨（アーチ） | 10 |
| 𓍢 | 巻いたロープ（コイル） | 100 |
| 𓆼 | 蓮の花（ロータス） | 1,000 |
| 𓂭 | 指 | 10,000 |
| 𓆐 | オタマジャクシ | 100,000 |
| 𓁨 | 座る神（ヘフ） | 1,000,000 |
https://miramiku.github.io/numerals/エジプト数字は加算方式で、同じ記号を繰り返して数を表します。記号の順序は自由ですが、通常は大きい値から小さい値へ並べます。
以上を踏まえて、今回のヒエログリフ数字を解読すると以下になります。
| 記号 | 意味 | 値 | 個数 | 小計 |
|---|---|---|---|---|
| 𓆼（蓮の花） | 1000 | 1000 | 1 | 1000 |
| 𓍢（巻いたロープ） | 100 | 100 | 4 | 400 |
| |（縦線） | 1 | 1 | 3 | 3 |
よって、数1403が得られます。
これを素因数分解すると、「1403=23×61」が得られます。
したがって、すべての数を特定して、その素因数分解までできました。ちなみに、Linuxコマンドで複数の数を一気に素因数分解するには以下のようにfactorコマンド[3]factorコマンドは coreutils パッケージに含まれており、ほとんどのLinuxディストリビューションで標準インストールされています。にまとめて渡します。
$ factor 74 69 6 55 1403
74: 2 37
69: 3 23
6: 2 3
55: 5 11
1403: 23 61
5つの数字の素因数分解をまとめてみます。
| 記数法 | 数値 | 素因数分解 | 左の素数 | 右の素数 |
|---|---|---|---|---|
| ローマ数字 | 74 | 2 × 37 | 2 | 37 |
| ギリシャ数字 | 69 | 3 × 23 | 3 | 23 |
| マヤ数字 | 6 | 2 × 3 | 2 | 3 |
| ヘブライ数字 | 55 | 5 × 11 | 5 | 11 |
| ヒエログリフ数字 | 1403 | 23 × 61 | 23 | 61 |
解読6
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
メッセージの3-4行目を読みます。
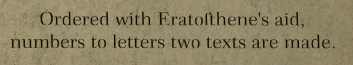
Ordered with Eratofthene's aid,
numbers to letters two texts are made.
和訳は次のとおりです。
エラトステネスの助けを借りて順序づけ、
数字を文字に変え、2つのテキストが作られる。
“Eratosthenes’s aid"（エラトステネスの助け）とは何なんでしょう。
エラトステネスは、ヘレニズム時代のエジプトで活躍したギリシャ人の学者です。
https://ja.wikipedia.org/wiki/エラトステネスエラトステネスやその業績から連想するのは、「エラトステネスの篩」「地球の円周の測定」「地理学の確立」が挙げられます。
これまで素因数分解や素数を扱ってきたので、おそらく「エラトステネスの篩」を連想するのが正解なのでしょう。これは、素数を見つける最古のアルゴリズムとして、数学教育で広く教えられています。具体的に説明すると、指定された整数以下のすべての素数を発見するための方法です。
https://ja.wikipedia.org/wiki/エラトステネスの篩ところで、メッセージには"Ordered"（順序づけ）という指示がありました。ここから、素数を順番に番号付けすることがわかります。
2＝1番目、3＝2番目、5＝3番目、…
さらに、"numbers to letters"（数字を文字に）とあります。ここから、その番号（インデックス）をアルファベットに対応させればよいとわかります。
1番目＝A、2番目＝B、3番目＝C、…
以上を組み合わせた表は以下になります（A=1）。
| 素数 | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 順番 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 文字 | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
この表を使って「素数⇒インデックス⇒文字」に置き換えていきます。
| 記数法 | 数値 | 左の素数 | 右の素数 |
|---|---|---|---|
| ローマ数字 | 74 | 素数2 ⇒インデックス1 ⇒’A’ | 素数37 ⇒インデックス12 ⇒’L’ |
| ギリシャ数字 | 69 | 素数3 ⇒インデックス2 ⇒’B’ | 素数23 ⇒インデックス9 ⇒’I’ |
| マヤ数字 | 6 | 素数2 ⇒インデックス1 ⇒’A’ | 素数3 ⇒インデックス2 ⇒’B’ |
| ヘブライ数字 | 55 | 素数5 ⇒インデックス3 ⇒’C’ | 素数11 ⇒インデックス5 ⇒’E’ |
| ヒエログリフ数字 | 1403 | 素数23 ⇒インデックス9 ⇒’I’ | 素数61 ⇒インデックス18 ⇒’R’ |
解読7
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
↓↓下にスクロール↓↓
メッセージの5-6行目を読みます。
Take the first of each in sequence,
to this proof lend credence.
以下がその和訳になります。
順番にそれぞれの最初を取れ、
この証明に信を与えよ。
“first of each in sequence"は、素因数分解で得られた素数を順番に変換していく過程を指していると解釈できます。
左の素数たちから得られた文字列は"ABACI"、右の素数から得られた文字列は"LIBER"になります。
2つの文字列"ABACI"＋"LIBER"でGoogle検索すると、"Liber Abaci"（『算盤の書』）がヒットします。
“Liber Abaci"（『算盤の書』）は、1202年にレオナルド・フィボナッチ（Leonardo Fibonacci）が発表した書物です。アラビア数字とインド式計算法をヨーロッパに紹介しました。
以上で解読は終了です。